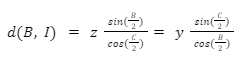Inscribed Circles of a Triangle and Their Radii

Inscribed circles of a triangle and their radii fit inside a triangle touching three of its sides. So, triangles with sides and circles with radii that are whole numbers are discussed in this article. Similarly, we have found results for isosceles triangles and right-angled triangles. There are three Pythagorean triplets here. Their angles are right angles, and their incircles have a radius of one and two units, respectively. Also, let us see if we can identify a right-angled triangle with sides that are primitive Pythagorean triples, with a radius of 3 units around its circumference. 

What Are Inscribed Circles of a Triangle?

An inscribed circle of a triangle or an incircle is a circle where the three sides of a triangle are its tangents. Inscribed circles of a triangle and their radii are contained within the triangle. In its most precise form, the circle inscribed inside the triangle will touch all three points of the sides of the triangle exactly once. Circles are defined by their centres, which is the meeting point of all angle bisectors of the triangle. This point is known as an incentre.

Construction of Inscribed Circles of a Triangle and Their Radii

You will need a ruler and a compass to draw an inscribed triangle. An inscribed circle is constructed in the following way:

1. Construct a triangle of specific dimensions.
2. Draw an angle bisector of one angle of the triangle. 
3. Draw the angle bisector of another angle of the triangle. The two bisectors will meet at a point inside the triangle. Say, the point is named O.
4. Draw a perpendicular from O to any of the sides of the triangle. Let the perpendicular intersect that side at X. 
5. Now, take OX as the radius on your compass and draw an entire circle around O. 

This way, you can easily construct inscribed circles of a triangle and their radii. In this case, the centre of the inscribed circle, or the incentre, is O. The radius of the incircle is OX. That means we have constructed the incircle on point O with a radius equal to OX. Thus, all three sides of the triangle touch the inscribed circles of a triangle and their radii.

Distance from Vertex to the Centre of an Inscribed Circle of a Triangle

Let us assume that ABC is a triangle. Now, suppose it has an incircle with a radius R and centre I. Also, let the lengths of AB, BC, and CA be x,y, and z, respectively. Then, we can calculate the formula for the distance between a vertex of the triangle and the incentre. 

It is given as:

Trilinear Coordinates in Inscribed Circles

We can also find the trilinear coordinates for inscribed circles of a triangle. The trilinear coordinates for any point inside the triangle are the ratio of all distances from the point to the sides of the triangle. 

In the case of an inscribed circle of a triangle, the incenter lies at the same distance from all three sides of the triangle. Or rather, the distance between the incentre and a side of the triangle is constant for that triangle.

For this reason, the trilinear coordinates for the incentre of an inscribed triangle are:

1:1:1

Barycentric Coordinates in Inscribed Circles:

Now, many would be unaware of the barycentric coordinates. Well, these coordinates of a point inside a triangle give weights such that the point is the weighted average of the triangle’s vertex. 

If we consider the lengths of a triangle AB, BC, and CA as  x,y, and z, respectively, then the barycentric coordinates for its inscribed circle would be:

a:b:c

Moreover, using the laws of sines, we can write this as: 

sin A:sin B:sin C

This gives us the barycentric coordinates of inscribed circles. 

Conclusion

Triangles make the three tangents of an inscribed circle, also known as the incircle. Incircles are the largest circles within a triangle, and their centres are known as incentres. The circle’s centre is located at the intersection between its three angle bisectors. The radius of the inscribed circle is called the inradius, which is given by r = K/s. Here, K represents the area of the triangle, and s represents its semiperimeter. In three places, the angle bisector intersects the opposing sides. 

In the above sections, we learned the different concepts related to inscribed circles of a triangle and their radii. These are very important for higher courses in geometry.