Profile
Settings
Refer your friends
Sign out
The equation in standard form is a form of a linear equation which consists of two variables with the power of one and three constants which are integers. These variables are expressed in the form of x-terms and y-terms (not always compulsory), and they are on the same side of the equation. Another linear equation is the slope-intercept form of the equation. It is used to evaluate the straight line equation when the slope of the line and intercept it is forming with the y-axis. Let’s go through both the form of equations and their conversion in maths.
Linear equation
Before going through the equations of the linear form, it is essential to know what a linear equation is. Thus, a linear equation is one in which all the variables have the power equal to one. No variable has a power greater than or smaller than one. The equation is written with the help of variables and constants where the variable has the power of one, and the constant is the integers.
Forms of Linear Equation
A linear equation has three forms, namely standard form, slope-intercept form, and point-slope form. Today we will learn about standard form and slope-intercept form.
The standard form of linear equation
The standard form is the linear equation consisting of two variables and the coefficients (constants).
Let us take x and y as the integers with the power of one, and a, b, and c are the integer coefficients.
Thus the standard form of the equation becomes ax + by = c.
Here ‘a’ should be a positive integer, whereas b and c can be the positive or negative integers.
The standard form of the equation helps find the value of x and y-intercepts. Intercepts tell us the point through which the graph crosses the x- and y-axis. To find the x-intercept, you have to substitute a 0 for the y; to find the y-intercept, you have to substitute a 0 for the x.
Slope-intercept form
This equation is used when the slope of the line is given. This is the most commonly used form of linear equations. It is represented by
y = mx + c
Where,
m is taken as the slope of the line, defined as the ratio of the change in the y coordinate to the corresponding change in the x coordinate between two different points on the line.
c is the y-intercept defined as they-coordinate where the line or curve, or surface intersects the y-axis.
x is the x-axis coordinate, and y is the y-axis coordinate.
For example, if y = 4x + 10,
then the slope, m = 4 and y- intercept = 10
If we take a straight line parallel to the x-axis, then the value of the x-coordinate will become 0. Thus, by substituting the value of the x-coordinate in the slope-intercept equation, we get,
y=c
Whereas, if the straight line is parallel to the y-axis, then the value of the y-coordinate will become zero. Thus, by substituting the value of the y-coordinate in the slope-intercept equation, we get,
mx+c = 0
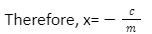
Now by the definition of slope, we know that,
Slope =m = (y – y1)/(x2 – x1)
Thus we can conclude that the slope shows the distance covered by the line along with the x-axis and the point to which the line has risen in the plane. The slope of the line is also referred to as gradient.
Standard Form to Slope-Intercept Form
Thus, we have seen from the above description that slope-intercept form is the more important form, so let’s convert Standard Form to Slope-Intercept Form,
To find slope-intercept form, let’s convert the following standard form equation to slope-intercept form,
8x -2y=16,
We need y to be isolated, so subtract both sides with 8x,
(8x – 2y)- 8x= 16-8x
-2y = 16-8x
Now we are left with -2y on the left. So, let’s divide both sides by -2 to isolate the y:
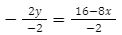
y= -8+4x
Now rearranging the equation in y = mx + b format, we get equation in slope-intercept form
y= 4x-8.
Conclusion
Thus from the above description of standard form and slope-intercept form of the equation, we can conclude that both the equations consist of the variables with power one and constants which are integers. The slope-intercept form is the most widely used equation. This equation can be used to find out the slope, x-coordinate, and y-intercept. The standard form of the equation is useful in finding the x-intercept and y-intercept easily when the slope is not given. The standard form of the equation can be converted to slope-intercept form.
