Profile
Settings
Refer your friends
Sign out
Function of Trigonometry
In mathematics, the real functions that denote the several angles of a right-angled triangle are termed trigonometric functions. They are alternatively also known as goniometric functions or circular functions. As the trigonometric operations repeat their values at fixed intervals (2π), they are also termed periodic functions. Geometrical trigonometric functions are applied in solid mechanics to determine periodic waves and oscillations.
In modern sciences, the trigonometric functions which are abundantly used are the sine, the tangent, and the cosine. Their reciprocal angles which are the cosecant, the cotangent, and the secant respectively are used less frequently.
Major Trigonometric Operations
Primarily modern mathematics deals with three basic trigonometric functions namely sine, tangent, and cosine. Three more functions are derivable from the above circular functions, they are cosecant, cotangent, and secant respectively. To understand all of them we will take a right-angled triangle named PQR.
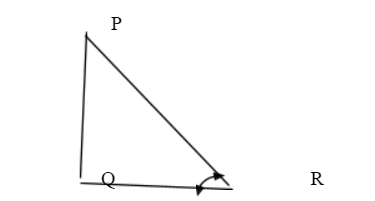
All the trigonometric functions will be discussed in association with the angle R.
∠R is situated opposite to the perpendicular PQ of the right-angled triangle PQR.
Side PQ is the hypotenuse of the △PQR.
Side QR is the base of the triangle.
1.Sine: The ratio between the opposite arm of an angle in a right-angled triangle and its hypotenuse provides us with the sine of that specific angle. In the above specimen side, PQ is drawn opposite to the ∠R while PR is the hypotenuse of △PQR.
∴ sin R = PQ/PR
2.Tangent: The ratio between the length of the opposite arm of the concerned angle in a right-angled triangle and its adjacent side gives us the tangent of that angle. Here, QR is the adjacent side of ∠R. Also the side PR is adjacent, but we do not consider the hypotenuse in this case.
∴ tan R = PQ/QR
3.Cosine: In a right-angled triangle, the cosine function can be simply determined by finding the ratio between the length of the adjacent arm of the concerned angle and the hypotenuse. In the case of triangle PQR, cos R = QR/PR.
Three other trigonometric functions are applied in less frequency. These are derived from the above three basic functions and each of them is the reciprocals of their parent functions.
As they are reciprocals, we can easily deduce their value by flipping the ratio.
Cosec R = 1 / sin R [ cosec function is the reciprocal of sin function]
∴ cosec R = PR / PQ
Similarly, we can deduce the sec function of ∠R from cosine R.
Sec R = 1 / cos R
∴ sec R = PR / QR
Cotangent or cot function is the reciprocal of tangent.
∴ cot R = 1 / tan R
or, cot R = QR / PQ
These are the trigonometric formulas for each of the angular functions.
Trigonometric Identities
Trigonometric identities are some key formulas that help us to solve several equations when the standard trigonometric functions are used in any expression. These identities satisfy each value of the variables associated with the trigonometric operation. The only condition is the triangle must be right-angled. Complex geometric problems are simplified to a great extent when we apply these trigonometric identities.
We can classify trigonometric identities into eleven types:
1.Reciprocal identities
An example of reciprocal identity: sin β = 1/ cosec β
2. Pythagorian identities
Example : 1 + tan² R = sec² R
3.Identities of trigonometric opposite angles
Cot (-β) = – cotβ, sin (-α) = – sin α and so on for the other trigonometric functions.
4.Trigonometric identities involving complementary angles
Examples are: Tan (90 – R) = Cot R
Cot ( 90 – R) = Tan R
5.Ratio trigonometric identities
Example : Tan α = sin α/ cos α
6.Trigonometric identities involving supplementary angles
These identities associate the angles whose sum is equal to 180°. For example, sec (180° – β) = – sec β
7.Trigonometric functional identities of products
For the angles P and R of the above △PQR, sin P. sin R = [cos (P- R) – cos (P + R)] /2
8.Product-sum identities
For the angles P and Q,
sin P + sin Q = 2 sin (P + Q) /2. Cos (P – Q) /2
9.Double angle identities
The equation tan 2β = (2 tan β) / (1 – tan² β) holds true if the angle β is doubled.
10.Half angle identities
Cos (β/2) = ±√(1 + cos β)/2
This equation is true if the angle denoted by variable β is halved.
11.Trigonometric identities – Sum and difference
Tan (P + R) = (tan P + tan R) / (1 – tan R. tan P)
Conclusion
The modern definition of trigonometric functions does not explain them only in case acute angles. We can assess the domain of the functions on a complex plane using trigonometric operations. An alternative superscript of – 1 gives the inverse functions of standard trigonometric functions.
