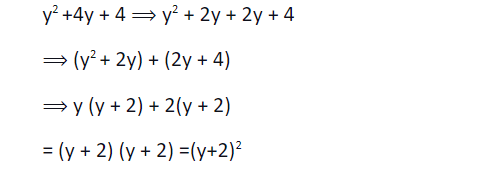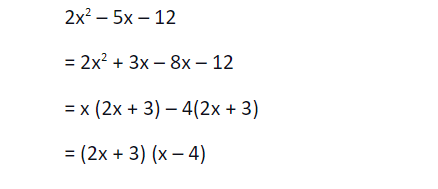Factoring polynomials by grouping

Factoring polynomials can be understood as the reverse procedure of the multiplication of factors of polynomials. An expression of the form axn + bxn-1 + ….+kx+ 1, where each variable is accompanied by a constant as its coefficient, is called a polynomial of degree ‘n’ in variable x. 

Therefore, a polynomial is an expression in which an addition or a subtraction sign separates a combination of a constant and a variable. Factors of polynomials are zeros of polynomials, which are represented in the form of another linear polynomial. After factoring a polynomial, the remainder will be zero if we divide the polynomial with any of its factors. The factors of the polynomials, when multiplied, produce the original polynomial.

Factorisation of binomials using the grouping method

A binomial is an expression that has two terms combined by either addition or subtraction sign. To factor a binomial, the following rules can be applied:

• ab + ac = a (b + c)

• a2– b2 = (a – b) (a + b)

• a3– b3 = (a – b) (a2 + ab + b2)

• a3+ b3 = (a + b) (a2 – ab + b2)

Illustration

1. Polynomial to factorise is 6a2b + 4bc using the grouping method.

Using the rule: ab + ac = a (b + c)

We get:

6a2b + 4bc = 2b (3a2 + 2c)

2. Polynomial to factorise is x6 – 64 using the grouping method.

Using the rule: a3+ b3 = (a + b) (a2 – ab + b2)

We get:

x6 – 64 = (x3)2 – 82

= (x3 + 8) (x3 – 8) = (x+2) (x2 − 2x + 4) (x − 2) (x2 + 2x + 4)

Factorisation of trinomials using the grouping method

To factor a trinomial of the form mx2 + nx + p by grouping, we perform the following steps:

Step 1: We find the product of the first coefficient ‘m’ and the constant ‘p’.

⟹ m p = mp

Step 2: Now we look for the factors of the ‘mp’ that add up to the coefficient ‘n’.

Step 3: Next we rewrite nx as a sum or difference of the factors of mp that add to n.

⟹ mx2 + nx + p = mx2 + (m + p) x + p

⟹ mx2 + mx + px + p

Step 4: Factor by grouping.

⟹ mx (x + 1) + p (x + 1)

⟹ (mx + p) (x + 1)

Illustration 

Polynomial to factorise using grouping method : x2 + 6x + 8

Step 1: Finding factors of 1×8 that add up to 6

Factors are 4 and 2.

Step 2: Now we can write the equation as:

x2 + 2x + 4x + 8

Step 3: Now we group the pairs as:

(x2 + 2x) + (4x + 8)

Step 4: Final step is to factor out the common factors

x(x + 2) + 4(x + 2)

=(x+4)(x+2)

Factorisation of quadrinomial using the grouping method

This method is also known as factoring by pairs. In this method, we distribute the given polynomials in pairs or group them in pairs to find zeros.

Illustration

Using the grouping method, the polynomial to factorise is x3 + x2 – x – 1.

Step 1: Split the polynomial into sets of two.

We can start with these sets of two (x3 + x2) + (–x – 1). Putting the plus sign between the sets, just like when we factorise trinomials.

Step 2: Find each set’s most significant common factor and factorise it out.

The square x2 is the greatest common factor of the first set, and –1 is the greatest common factor of the second set. After factoring out both of them, we get:

x2(x + 1) – 1(x + 1)

Step 3: Continue to factorise until it cannot be factored further.

The two terms we have created have the greatest common factor of (x + 1), which, when factored out, gives (x + 1)(x2 – 1).

Here, x2 – 1 is an identity of difference of squares that is a2 – b2= (a + b)(a – b) using which we get factors as (x+1)(x-1). This gives us a final factorisation of:

(x + 1)(x + 1)(x – 1), or (x + 1)2(x – 1).

Factorisation of polynomials using the grouping method

Factorisation by grouping is simply the process of grouping terms with common factors together before factoring.

• Check if the polynomial terms have the Greatest Common Factor (GCF). If yes, factor it out and include it in your final answer.

• Break up the polynomial into sets of two.

• Remove the GCF from each set.

• Lastly, determine if the remaining expressions can be factored further. 

Illustration

Polynomial to factorise is 2ax + ay + 2bx + by using the grouping method.

2ax + ay + 2bx + by

= a (2x + y) + b (2x + y)

= (2x + y) (a + b)

Conclusion

We can factorise a polynomial using many methods, most common among which are methods like factorisation using the greatest common factor method, factorisation using the grouping method, and factoring using algebraic identities. Further grouping methods use different approaches for binomial, trinomial, quadrinomial, and polynomials.