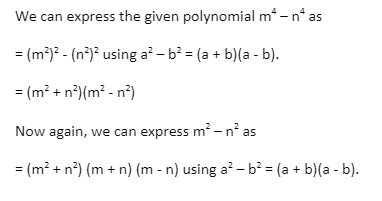Factoring Polynomials

The factorisation is a method to break arithmetic algebraic expressions into the product of their factors. When dealing with polynomials, the factors of the polynomials, when multiplied, produce the original polynomial. For example, the factors of x2 + 5x + 6 are (x + 2) (x + 3). The original polynomial was obtained by multiplying both x +2 and x+3. 

Factoring polynomials

Different methods for factoring polynomials are:

• Greatest Common Factor (GCF)

• Grouping Method

• Sum or difference in two cubes

• Trinomial method

• The difference in two squares method

• General trinomials

Among these methods, the three most basic and most used methods of factoring a polynomial are:

• Greatest Common Factor (GCF)

• Grouping Method

• Factorising using algebraic identities.

The identities frequently used for factorising a given polynomial are as follows:

• (a + b)2 = a2 + 2ab + b2

• (a – b)2 = a2 – 2ab + b2

• a2 – b2= (a + b)(a – b)

• (x + a)(x + b) = x2 + (a + b) x + ab

• (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca

• (a + b)3 = a3 + b3 + 3ab (a + b)

• (a – b)3 = a3 – b3 – 3ab (a – b)

• a3+b3+c3 – 3abc = (a + b + c)(a2 + b2 + c2 – ab – bc – ca)

Method 1: Greatest Common Factor (GCF)

We start by finding the greatest common factor of the given polynomial. It is equivalent to the reverse of distributive law, that is: P (Q + R) = PQ + PR

The reverse of distributive law can be written as: PQ + PR = P (Q + R)

Here p is the Greatest Common Factor of the above expression.

Illustration

Polynomial to factorise is 6x4 – 12x3 + 4x2 using the Greatest Common Factor method.

Step 1: Breaking down every term to its prime factor form, thus expanding the given original polynomial.

(23xxxx)- (223xxx)+ (22xx) 

Step 2: To find common factors to all the terms, this step helps determine the greatest common factor for the given polynomial expression.

Here, we can see one 2, and two x’s in every term:

Therefore the greatest common factor here is 2×2.

Step 3: To separate the greatest common factor by writing the greatest common factor out from every term, placing it in front of parentheses, and grouping the remaining inside the parentheses.

Now we get:

2xx (3xx-23x+2)

A simplified form of this above expression can be written as 2×2(3×2 – 6x + 2).

Step 4: To check if the polynomial is factored correctly, we can multiply the greatest common factor back to the remaining terms. If the original polynomial is obtained back, that proves the factorisation holds.

If we multiply the 2×2 inside the parentheses, we get 6x4 – 12x3 + 4x2. Now we can say with confidence that 2×2 is the GCF.

Method 2: Factorisation using the grouping method

This method is also known as factoring by pairs. In this method, we distribute the given polynomials in pairs or group them in pairs to find zeros.

Illustration

Polynomial to factorise is x3 + x2 – x – 1 using the grouping method.

Step 1: Breaking up the polynomial into sets of two.

We can start with these sets of two (x3 + x2) + (–x – 1). We put the plus sign between the sets, just like when we factorise trinomials.

Step 2: Find the greatest common factor of each set and factorise it.

The square x2 is the greatest common factor of the first set, and –1 is the greatest common factor of the second set. After factoring out both of them, we get:

x2(x + 1) – 1(x + 1)

Step 3: We continue to factorise until it cannot be factorised further.

The two terms we have created have the greatest common factor of (x + 1), which, when factored out, gives (x + 1)(x2 – 1).

Here, x2 – 1 is an identity of difference of squares that is a2 – b2= (a + b)(a – b) using which we get factors as (x+1)(x-1). This gives us a final factorisation of:

(x + 1)(x + 1)(x – 1), or (x+1)2(x – 1).

Method 3: Factorising using algebraic identities

Factorisation of a polynomial can also be done by using algebraic identities. The most common identities used for factorisation of polynomials are:

• (a + b)2 = a2 + 2ab + b2

• (a – b)2 = a2 – 2ab + b2

• a2 – b2= (a + b)(a – b)

Illustration

1. Polynomial to factorise is z2 + 6z + 9 using algebraic identities.

We can express z2 + 6z + 9 as 

= (z)2 + 2(z)(3) + (3)2 using identity a2+ 2ab + b2 = (a + b)2

= (z + 3)2

= (z + 3)(z + 3)

2. Polynomial to factorise is 4m2 – 12mn + 9n2 using algebraic identities.

We can express 4m2 – 12mn + 9n2 as 

=(2m)2 – 2(2m)(3n) + (3n)2 using identity a2– 2ab + b2 = (a – b)2

= (2m – 3n)2

= (2m – 3n)(2m – 3n)

3. Polynomial to factorise is 25x2 – 49 using algebraic identities.

We can express 25x2 – 49 as 

= (5x)2 – (7)2 using a2 – b2 = (a + b)(a – b).

= (5x + 7)(5x – 7)

Conclusion

We can factorise a polynomial using many methods, most common among which are methods like the greatest common factor method, the grouping method, and the algebraic identities method.