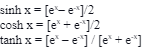Exponential and Hyperbolic Functions

Calculus is a discipline of mathematics that deals with continuous change and is one of the most significant areas of mathematics. Calculus is built on two key concepts: derivatives and integrals. The rate of change of a function is measured by its derivative, while the area under the function’s curve is measured by its integral. The integral collects the discrete values across a range of values, while the derivative explains the function at a given point.

Infinite calculus, or “the calculus of infinitesimals,” is another name for calculus. Infinitesimal numbers are numbers with a close to zero but not precisely zero. Classical calculus is the study of functions that change continuously.

Integral Calculus

The branch of calculus where we learn about integrals’ theory, properties, and applications is known as integral calculus. It is linked to differential calculus, and they form the basis of mathematical analysis. The fundamental theorem of calculus connects integral calculus with differential calculus.

Lengths, areas, volumes, total values, and the derivation of the formula for discovering antiderivatives are all covered in integral calculus.

Fundamental Theorem of Integral Calculus

Calculus’s fundamental theorem connects the principles of differentiating and integrating functions. The first part of the theorem – the first fundamental theorem of calculus – asserts that by integrating f with a variable limit of integration, one of the antiderivatives (also known as an indefinite integral) of a function f, say F, may be derived. This implies the occurrence of antiderivatives for continuous functions.

The integral of a function f over some interval may be calculated using its infinitely numerous antiderivatives, such as F, according to the second half of the theorem – the second fundamental theorem of calculus. There is an unlimited number since the integration constant, C, has an endless number of choices.

This aspect of the theorem is valuable in practice since it eliminates the need for numerical integration to compute integrals by utilizing symbolic integration to obtain the antiderivative of a function. A better degree of numerical accuracy is frequently the outcome of this.

The Fundamental Theorem of Integral Calculus is the most popular approach to assess definite integrals since it relates the derivative and the integral. It asserts in a nutshell that any continuous function over an interval has an antiderivative (a function whose rate of change, or derivative, equals the function). 

Integral Calculus Categories

The two types of integral calculus are as follows. They are as follows:

1. Indefinite Integral
2. Definite Integral

Exponential and Hyperbolic Functions

In engineering, physics, and mathematics, some even and odd combinations of the exponential functions ex and e-x appear so often that they are given unique names. Hyperbolic functions are similar to trigonometric functions in that they have the same names as trigonometric functions but with the letter ‘h’ added to the end of each name.

These unique functions are related to the hyperbola in the same way as trigonometric functions are related to the circle. As a result, they are referred to as hyperbolic functions collectively and as hyperbolic sine, hyperbolic cosine, and so on. They may be used as solutions to certain partial differential equations and modeling.

Consider tying two ends of a rope together and letting it dangle from the ceiling due to gravity. A hyperbolic cosine curve will arise due to the rope’s design.

Exponential and hyperbolic functions are defined by algebraic equations, including the exponential function (ex) and its inverse exponential function (e-x), where e is Euler’s constant. In addition to linear, quadratic, rational, and radical functions. An exponential function is a mathematical function of form f (x) = aex, where “x” is a variable and “a” is a constant that is termed the function’s base and must be more significant than zero. Bacterial growth is an example of an exponential function. Some bacteria multiply by doubling every hour. We may utilize hyperbolic functions to determine the distance in non-Euclidean geometry, estimating angles and distances in hyperbolic geometry.

We can find the hyperbolic functions using the formulas given below:

Using the reciprocal relation of these functions, we can find the other hyperbolic functions.

Exponential functions represent many scientific phenomena. Population increase, compound interest, and radioactive decay are all examples of uses for exponential functions. Radioactive decay is used to determine the age of ancient objects discovered at ancient finds. Exponential functions have a stable base with an independent variable that is an exponent. Exponents are used in the formulations of exponential functions. An exponential equation may take one of the two forms.

Conclusion

Calculus is a medium used by engineers to determine quantities like rate and areas. Calculus is the mathematical ‘backbone’ for dealing with mathematical problems where variables change with time. A basic understanding of calculus is required for further study and confidence in solving practical engineering problems. Physical systems that are modelled and use the ‘rates of change’ equations enable the physical system to be represented, an analysis to be performed, and a solution generated under specified circumstances.