Profile
Settings
Refer your friends
Sign out
The determinant can be considered the function associated with each square matrix with a unique number; the number can be real or complex depending on the nature of the matrix. The determinant is only applicable to square matrices, such as 2×2, 3×3, and 4×4.
Square matrix: It is defined as a matrix with the same rows and columns.
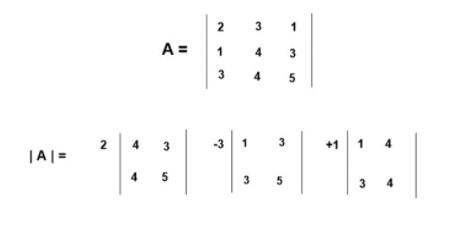
If matrix A = , then the determinant of a square matrix A represent as | A | = = det (A)
How to Solve For Determinants
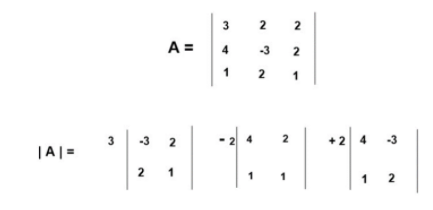
Evaluate Determinants of 3×3 Matrices or matrix of order three
Step 5) Calculate the value of the determinants
Application of 3×3 Determinants
1) Determinants of the matrix are used to find out the inverse of the matrix. If the determinant of any square matrix exists, which implies the inverse of that matrix also exists, we can find the inverse of that matrix by using cofactors.
2) Determinants are used to calculate the eigenvalue of any system in quantum computing.
3) It is also used to calculate the variance in any given system.
4) It is used to calculate the solution of any linear system, e.g. in the crammers rule, we have to use determinants to find the solution of a given linear system having the same number of variables and equations.
5) It is also used to check whether a triangle is collinear or not. If the area of the triangle is zero, then the triangle is collinear.
6) If the triangle’s vertices are known, it is possible to calculate the area of the triangle in determinant form using them. Suppose we have a triangle ABC with three vertices:
7) Determinant applications are used in the polynomial interpolation to various degrees.
