Profile
Settings
Refer your friends
Sign out
A derivative of a function is the rate of change of one variable involved in the function, say x with respect to corresponding change of another variable in the same function, say y. A derivative trigonometric function is the rate of change of a trigonometric function with respect to another variable. Usually all functions are derived using sinx and cosx functions and their derivatives.
Limits for trigonometric functions
Limits for trigonometric functions are like limits for other derivative functions only. The limits for trigonometric functions give the value of the function as the limit approaches towards a certain value of itself.
Some of the important limits of trigonometric functions to remember are:
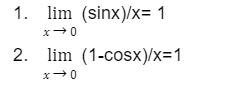
One important thing to note here is that when x approaches infinity in any of the trigonometric functions, limits do not exist for any of the six trigonometric formulas.
Derivation
To define a derivative of a function, we take a function f, a real valued function and a as a point in the function f’s domain.
Now, the derivative of f at a is defined as:
It is assumed here that the limits exist here.
The derivative of the function can be denoted as either df/dx or f’(x) commonly.
Common derivative formulas
Some formulas are directly applied in order to calculate the derivatives of a more complex function. The basic algebraic operations on derivation is applied as;
1.(u+v)’= u’+v
2.(u-v)’=u’-v’
3.(uv)’=u’v+uv’ This is commonly known as the product rule.
4.(u’v-uv’)/v2 This is known as the quotient rule.
Derivation of sinx and cosx
We can find the derivatives of sinx and cosx which can then be applied to solve for derivatives of other trigonometric functions.
For derivation of sinx,
let f(x)= sinx
Derivation of other trigonometric functions using sinx and cosx
For example, tanx can be calculated by using results of derivatives of cosx and sinx
As we know that tanx= sinx/cosx
Applying derivative formula both sides
d(tanx)/dx= d(sinx/cosx)/dx
Here we can assume u= sinx and v=cosx to make it simpler
Using the quotient rule (u/v)’ = (u’v-uv’)/v2
Substituting values of u and v in this quotient rule, we get
(sinx/cosx)’ = [(sinx)’cosx – sinx(cosx)’]/cos2x
We use derivatives of sinx and cosx and substitute them in the equation
(tanx)’= [ cosx.cosx – sinx(-sinx)]/cos2x
(tanx)’ = [cos2x+sin2x]/cos2x
Sin2x+ cos2x = 1 is an identity formula. Substituting this we get,
(tanx)’= 1/cos2x= sec2x
Formulas for trigonometric functions
The rest of the derivatives trigonometric function can be derived similarly by using derivatives of sinx and cosx. These six basic trigonometric derivatives are used to solve questions further.
Some of the important derivatives of trigonometric formulas are-
- d(sinx)/dx = cosx
- d(cosx)/dx = sinx
- d(tanx)/dx = sec2x
- d(cotx)/dx = -cosec2x
- d(secx)/dx= secx tanx
- d(cosecx)/dx= cosecx cotx
Examples:
- Calculate derivative of f(x)= 3sinx – 4cosx
Applying derivative function on both sides
f’(x)= d(3sinx – 4cosx)dx
Using (u-v)’ = u’-v’
f’(x)= d(3sinx)/dx – d(4cosx)/dx
We use derivatives of sinx and cosx and substitute them in the equation
f’(x)= 3cosx – 4(-sinx)
f’(x)= 3cosx+4sinx
Applications of trigonometric functions
Trigonometric functions are used to calculate tangent and normal of a given curve. We also use trigonometric functions to determine maximum and minimum values of a given function. Trigonometric functions have a lot of real life applications such as measuring heights of mountains, they are also used in construction of buildings, architectural places. Trigonometric functions are also used in determining a flight path for an airplane, another application can be found in calculating trajectory of moving objects like celestial objects, satellite navigation systems are also built on trigonometric functions, newer fields like computer graphics and in-game development are also applications of the same.
Conclusion
Derivative trigonometric function is the rate of change of a trigonometric function with respect to another variable. When x approaches infinity in any of the trigonometric functions, limits do not exist for any of the six trigonometric functions. Derivatives of sinx and cosx which are applied to solve for derivatives of other trigonometric functions. In mathematics, differentiated trigonometric functions find application in finding tangent and normal of a curve and also to calculate the maximum and minimum value of a function.
