Profile
Settings
Refer your friends
Sign out
What Is Derivative?
Derivative, the term is the fundamental method of calculating the alterations in the rate of any quantity in the numerator with respect to any other quantity placed in the denominator. It will not be wrong if we say derivatives are used to obtain the immediate instantaneous change that happens with any function.
This is how we define the derivative of the quantity y with respect to another quantity x.
{d (y) }/ {d (x)}
f ‘ (x), this is also a symbol to denote derivatives.
f ‘ (x) represents that there is one function y=f(x), and we are differentiating it with respect to other quantities x.
Derivatives have layers too. It simply means that we can find the derivative of an already differentiated function too, and this process can go to multiple loops if required. When we differentiate an original function or expression, then the resultant expression or function will be called the first derivative of that function.
Similarly, the number of times you differentiate the function, the name will change continuously from the first derivative to the second derivative, second to the third derivative, and so on.
What Is Geometric Interpretation?
Graphical Representation of a function is so important because it is used to observe and interpret the relationship between two variables and also interpret a common repeating pattern (if present) in a function.
You should know that the graph of any original function is not the same as the graph plotted of the derivative of that same function. And, as we go on differentiating the function again and again, the graph will not be the same and lose its similarity.
What Is Derivative Graph?
The first step is to choose two distinct points (let’s say P and Q) on the curve anywhere to the top or bottom doesn’t matter.
Joining P and Q with a straight line is called a secant line.
The next step involves connecting both the points P and Q to the X-axis as well as to the Y-axis with the help of straight lines.
The point at the X-axis where P is joining through a straight line is called “a” and the point at the Y-axis where P is joining through a straight line is called f(a).
Similarly, the point at the X-axis where Q is joining through a straight line is called “a+h” and the point at the Y-axis where Q is joining through a straight line is called f(a+h).
Draw a straight line along the x-axis from the point P in such a way that it intersects the vertical line between the x-axis and Q, name it as R.
Small “h” is the distance PR.
Hence, we can easily write down the coordinate of the P which is (a, f (a), and also the coordinates of Q which is (a + h, f(a + h).
The formula for finding differentiation is :
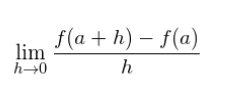
We can find out the coordinates of Q f(a+h).
If you observe the figure closely, you will see a triangle QPR. You know that QR is equal to f (a + h) – f (a) and PR is equal to h. Thus substituting these values in the differentiation limit formula:
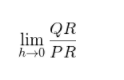
Since QPR is also a regular right triangle, we can find many unknowns. Tanθ = QR/PR.
Conclusion
To summarize the above-difficult technique for geometric interpretation of a derivative function, the tangent is the geometrical or graphical representation of the derivative. Distinct functions have diverse derivatives, as we all know. As a result, the meaning of these derivatives on the graph will vary depending on the situation. However, regardless of the function type or derivative, all derivatives have one thing in common: they all take the shape of a tangent line to the function graph, or we should also remember that derivatives at a point on the curve also give you the slope of the tangent line. I wish you learned the very basics of what is a derivative, how to find derivatives, what is geometrical interpretation, and how to find different unknown variables from them.
