Profile
Settings
Refer your friends
Sign out
The derivative of a function of a real variable in mathematics describes the sensitivity of the function value to a change in its argument. Derivatives are a fundamental tool for finding maxima minima and for understanding the nature of functions.
The derivative is a function itself; it describes in detail how much one quantity is changing in terms of another quantity. Its properties have many uses in mathematics and in other sciences, as well as in engineering.
This article aims to teach you about derivatives and how they can be used to study transforming functions (both linear and nonlinear).
What is Derivative?
A derivative is a function that tells you how much one quantity is changing at a given point compared to another quantity.
The derivative is a fundamental concept of calculus. Intuitively, the derivative represents the rate of change or slope of the function at a given point. The derivative is defined as the limit of the difference quotient Δy/Δx as Δx approaches zero.
What is Derivative Formula?
The Derivative formula is used to find a derivative is known as Differentiation. The Formula for the Derivative is obtained for a variable ‘x’ having an exponent ‘y’. The exponent may be an integer or a Rational Fraction
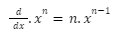
Rules of Derivative
There are some rules needed to be followed. These rules are the formulas that are used in the different levels and aspects of derivatives.
Derivation of Derivative Formula
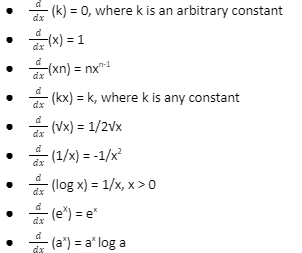
Derivative Formula for the trigonometric function
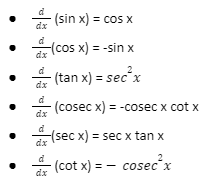
Types of the Derivative
A derivative is classified on the basis of the order
- First Order
- Second Order
First-Order Derivative
The first order derivatives indicate the direction of the function, that is, whether the function is increasing or decreasing. The first derivative maths or first-order derivative can be interpreted as an instantaneous rate of change. It can also be predicted from the slope of the tangent line at x = a.
Second-Order Derivative
To acquire an understanding of the shape of the graph for a given function, second-order derivatives are used. Concavity can be used to categorize the functions.The concavity of the given graph function is classified into two types, namely, downward concave curve and upward concave curve. An inflection point is found where the first and second-order derivatives are zero (at the endpoints).
Applications of the Derivative
Derivatives are the rates at which the quantity is changing with respect to time. So, we have done integration to find the displacement from its velocity and from displacement to get the distance travelled by a body. Similarly, we use derivatives to find the rate of change of one quantity with respect to another quantity which is obtained by differentiating suitable functions.
Point of Inflection
If f ‘(x0) = 0 or f’”(x0) does not exist at points where f'(x0) exists and if f”(x) changes sign when passing through,
x = x0 then x0 is called the point of inflection.
- If f”(x) < 0, x ∈ (a, b), then it is concave Downward.
- if f” (x) > 0, x ∈ (a, b), then it is Concave Upward
In Real Life
- check the temperature variation.
- determine the speed or distance covered
- Deriving the Equations in Physics
- study of Seismology like to find the range of magnitudes
- calculate the profit and loss in business
Approximation or Finding Approximate Value
Calculus uses derivatives to approximate any change in a quantity. If we need the rate of change, considering delta △ x as very small, the derivative gives this value.
dy/dx = △x = x.
Monotonicity
A function is called monotonic if it is either entirely increasing or entirely decreasing. That is to say that a monotonic function has the same sign throughout its entire domain. If a function is neither increasing or decreasing in its entire domain, then it is considered non-monotonic.
- f'(x) will be positive when the function is increasing.
- f'(x) will be negative when the function is decreasing.
- f'(x) will be zero when the function is at its maxima or minima.
