Profile
Settings
Refer your friends
Sign out
In this article, we will learn about continuity and differentiability. The concept of continuity refers to a function that changes through time without abrupt gaps or leaps. when the function is continuous there if a limit occurs and is equal to the function’s outcome at that time. As in topology, continuity may be described in terms of sets. According to mathematics, a differentiable function on a real variable is one whose derivative happens at every point in its domain. In other words, on the graph of such a function, each interior location in the domain does have a non-vertical tangent.
Definition of continuity
In mathematics, continuity is a definitive expression of the intuitive sense of a function that varies without abrupt breaks or leaps. A function is a relationship between the values of an independent variable and the values of a dependent variable.
The geometrical significance of continuity is if a function is continuous, it does not have breaks in its graphing, but when it is discontinuous, it does. The point at which discontinuity seems to be there is the position at which the function’s graphs break. If a limit exists and is equivalent to the function’s result at that moment, the function is continuous there.
A somewhat more abstracted definition of continuity may be expressed in terms of sets, as in topology, by stating that each open set of y-values corresponds to an open set of x-values. (A set is “open” if every one of its components has a completely inside the set “neighbourhood,” or region encircling it.) Continuous functions are by far the most fundamental and most-studied category of functions in applied mathematics, as well as the ones that occur most frequently in physical settings.
Differentiation
In mathematics, differentiation is the process of determining a function’s derivatives, or rate of change. In contrary to the abstract character of the theory that underpins it, differentiation may be achieved using just algebraic operations, requiring only three fundamental derivatives, 4 principles of operations, and a working grasp of functions.
Differentiability
A differentiable function of a real variable is the one whose derivative occurs at each point in its domain, according to mathematics. In other words, each interior point in the domain of a differentiable function seems to have a non-vertical tangent line on its graph.
If a function’s derivative occurs at each point through its domain, it’s said to be differentiable, but what does it mean?
It indicates that a function may be differentiated everywhere, at which a derivative is specified.
The function is differentiable as long as the derivative can be evaluated at any point on the curve.
Formula for differentiability
Assume that f is a function but that c is a domain point. 0 defines the derivative for f at c.
At c, the derivation of the function f is expressed as-
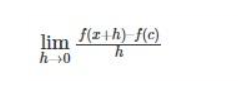
If f becomes differentiable at x0, it also has to be continuous at that point. Any differentiable function, in particular, must be continuous across its domain. The opposite is not true: a continuous function does not have to be differentiable. A function with such a bend, vertical tangent or cusp for example, maybe continuous but not differentiable at the anomalous position.
Most functions encountered in practice contain derivatives at all or almost all points. Stefan Banach’s conclusion, on the other hand, argues that a set of functions with a derivative at a certain point is a small subset of the field among all continuous functions. Unofficially, this indicates that among continuous functions, differentiable functions are exceedingly unusual. The Weierstrass function is the earliest documented case of a function that is continuous everywhere else but differentiable nowhere.
Continuity and differentiability
If a derivative exists and is in itself a continuous function, the function is said to be continuously differentiable. Although a differentiable function’s derivative doesn’t have a jump discontinuity, the derivative might have an important discontinuity. For instance, consider the function
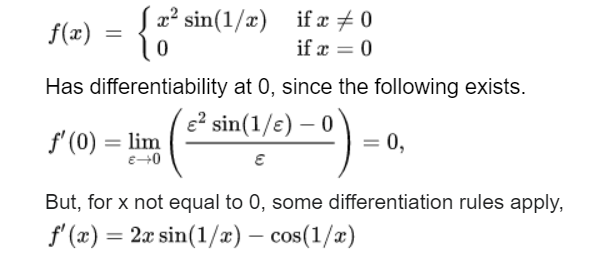
Conclusion
We’ve discussed continuity and differentiability. Read the article thoroughly to grasp the concepts fully and practice as many questions on the topic as you possibly can. Mathematics is simple when we understand the basics and practice rigorously and diligently. Make a note of the formulas given above and try to memorize them through spaced repetition method.
