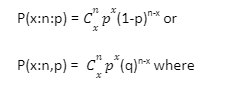Binomial Distribution

The binomial distribution, which predicts the odds of obtaining one of two outcomes given a set of parameters, is an example of a typical probability distribution. It is a summary of the number of trials that were done with the same chance of attaining a particular outcome as the others. The value of a binomial may be calculated by multiplying the number of independent trials by the number of successes.

What is Binomial Distribution?

• The distribution of random variables in probability is called Binomial distribution.
• Toss two coins you might get the four possible experiments like (head-head), (tail head), ( head-tail), (tail)
• Consider the occurrence of the head as success. Then 

n- getting number of the head is given as 

n(x) = 0,1 or 2 head is the binomial random variable

Here, the probability of occurrence of the head is distributed.

The above table shows the probability of getting one head in the single flip of two coins is 1/2. If we toss the three-coin, then there might be eight possible outcomes like 

• (head head head)
• (head-tail)
• (head-tail tail)
• (head-tail tail)
• (tail head)
• (tail head tail)
• ( tail head)
• (tail tail tail)

Consider the occurrence of the head as success. Then 

n- getting number of head is given as 

n(x) = 0,1, 2or 3 is the binomial random variable

• P( zero heads x=0) = 1/8
• P( one head, x=1) = 3/8
• P(two head, x=2) = 3/8
• P(three head, x=3) = 1/8

Negative binomial distribution

Hre is an example of a clear understanding of negative binomial distribution.

Suppose throw dice the occurrence of all three is considered as the failure and non-3’s are Success ‘r’ is the letter used to demonstrate failure.

If the dice are thrown frequently until 3 appears four-time, which means r = four failures, then the binomial distribution of the number non-3’s that arrived would be the negative binomial distribution.

Binomial distribution formula

The binomial distribution formula is given by 

X- random variable and it is given by

where p – the probability of success

q – is the probability of success

n – number of trails 

The binomial distribution is written as

where

• p – the probability of success
• n – number of trails 
• X – is the number of success rate

Bernoulli trials

• The probability of getting only two results is called Bernoulli trials. 
• P – is the success probability
• q=1-p is the probability of failure

For example

1. Gender revival: boy or girl
2. The probability of rain today: Yes or no
3. Tossing a coin will have only two outcomes: head or tail
4. The eighth card of a well-shuffled deck is a diamond. The possible outcomes of the eighth card in diamond are Yes and No.
5. Rolling a die where a ‘3’ is a ‘success’ and all other numbers are considered as ‘failure.’

PMF of bernoulli distribution

P(X=x) where

• p for x=1
• 1-p for x=0

Condition of Bernoulli trials

Here are some of the conditions of the Bernoulli trials that are listed below

1. The trait should be finite in case of infinite ist is not applicable
2. The trial should not be dependent on one another
3. One two possible outcomes should be in the trial – Yes(success) or no(failure)
4. In every trial, the probability should be the same.

Bernoulli trial formulas

Here are important formulas related to Bernoulli trials

1. If X is the random variable in the Bernoulli distribution then

P(X=1) = p,

P(x=0) = 1-p = q

2) In a binomial experiment, X is the number of successes then

n- independent trail

p(X=k) = 

where

• p – is the probability of success rate
• q- is the probability of failure

3) the PMF(probability mass function) for Bernoulli distribution where n=1

y – random variable

p – is success probability

f(y, p) = {p, if y = 1 and q = 1- p, if y = 0}

OR

f(y, p) = py (1 – p)1-z, for y = 0, 1

4) If Y is the Bernoulli random variable, then the expected value(mean) is

E(Y) = p

5) If Y is the Bernoulli random variable, then the variance is

Var[Y] = p(1-p) = pq

Conclusion

The binomial distribution is used in statistics as a building component for dichotomous variables, such as the likelihood that either candidate A or B would emerge in position one on the midterm exams, which are dichotomous variables. It also represents the probability of an event happening, provided the given criteria are met. If you wish to use the binomial probability formula, you must first understand the binomial distribution. These regulations must be observed at all times throughout the operation.