A number system can be described as a process of writing and expressing numbers. In a number system, there are four different types of the number system, and the binary system of numbers is one of those with base 2. These are mainly used in computer applications for programming and coding purposes. Every time the input is given to the computer system in the decimal form, it is further converted into binary digits, performs its functions and provides the required output.
This article talks about the binary system of numbers. You will find brief information on the concept of the number system in Maths, a thorough explanation of bits in binary conversion, and other related topics. So, let’s start by describing the conversion of a number in a decimal system to a binary system in the Maths study material.
What is a number system in maths?
The numeral system, commonly known as the number system, is the system that constitutes numbers. It is often referred to as a mathematical representation of numbers using a given set of digits or numbers in a consistent manner. It promotes easy arithmetic operations such as addition, subtraction, multiplication, and division. In other words, the number system is a way of representing numbers in computer architecture. There are four types of numbers in a number system. These include –
Octal numbers with base 8
Binary numbers with base 2
Decimal numbers with base 10
Hexadecimal numbers with base 16.
Explain the binary system of numbers
According to mathematics and digital electronics, the binary system of numbers can be expressed as a number written in the base 2 numeral system or the binary system. Also, it is used for describing the numeric values of two different symbols, including 0 (zero) and 1 (one). Today, all computer systems have binary systems in them also; every digit is referred to as a bit.
The bit in binary number
Every single digit in the binary system is referred to as the bit. In a binary system, there are multiple bits, such as 1001 is a four-bit binary number, 101 is a three-bit binary number, and 11 is a two-bit binary number.
Binary numbers table
Number | Binary Number | Number | Binary Number | Number | Binary Number |
1 | 1 | 11 | 1011 | 21 | 10101 |
2 | 10 | 12 | 1100 | 22 | 10110 |
3 | 11 | 13 | 1101 | 23 | 10111 |
4 | 100 | 14 | 1110 | 24 | 11000 |
5 | 101 | 15 | 1111 | 25 | 11001 |
6 | 110 | 16 | 10000 | 26 | 11010 |
7 | 111 | 17 | 10001 | 27 | 11011 |
8 | 1000 | 18 | 10010 | 28 | 11100 |
9 | 1001 | 19 | 10011 | 29 | 11101 |
10 | 1010 | 20 | 10100 | 30 | 11110 |
Calculating binary numbers
Let the number be 1235.
Here,
Thousands | Hundreds | Tens | Ones |
1 | 2 | 3 | 5 |
This means that
1235 = 1 × 1000 + 2 × 100 + 3 × 10 + 5 × 1
Given,
1000 | = 103 = 10 × 10 × 10 |
100 | = 102 = 10 × 10 |
10 | = 101 = 10 |
1 | = 100 |
It can be described as,
Thousands | Hundreds | Tens | Ones |
103 | 102 | 101 | 100 |
1 | 2 | 3 | 5 |
Hence,
1235 = 1 × 1000 + 2 × 100 + 3 × 10 + 5 × 1
= 1 × 103 + 2 × 102 + 3 × 101 + 5 × 100
There are different methods and formulas through which the decimal numbers can be converted into binary numbers. Here are the following steps through which the decimal numbers can be converted into binary numbers.
Step 1: The given decimal number should be divided by 2 to give the result leaving the remainder behind.
Step 2: In case the decimal number is even, let’s say 3,5,7,9, and so on, the remainder will be zero.
Step 3: In case the decimal number is odd, let’s say 2,4,6,8, and so on, the remainder will always be 1.
Step 4: By placing the reminders in a single order so that the Least Significant Bit is placed at the top whereas, the Most Significant Bit is at the bottom. In such cases, the required binary number can be obtained.
Converting the number 294 in the binary number –
Divide by 2 | Result | Remainder | Binary Value |
294 ÷ 2 | 147 | 0 | 0 (LSB) |
147 ÷ 2 | 73 | 1 | 1 |
73 ÷ 2 | 36 | 1 | 1 |
36 ÷ 2 | 18 | 0 | 0 |
18 ÷ 2 | 9 | 0 | 0 |
9 ÷ 2 | 4 | 1 | 1 |
4 ÷ 2 | 2 | 0 | 0 |
2 ÷ 2 | 1 | 0 | 0 |
1 ÷ 2 | 0 | 1 | 1 (MSB) |
Decimal to binary table
Here is the decimal to binary conversion table –
Decimal Number | Binary Number |
0 | 0 |
1 | 1 |
2 | 10 |
3 | 11 |
4 | 100 |
5 | 101 |
6 | 110 |
7 | 111 |
8 | 1000 |
9 | 1001 |
10 | 1010 |
11 | 1011 |
12 | 1100 |
13 | 1101 |
14 | 1110 |
15 | 1111 |
16 | 10000 |
17 | 10001 |
18 | 10010 |
19 | 10011 |
20 | 10100 |
Binary addition
Adding two binary numbers will give rise to the binary number in itself.
Binary Numbers | Addition | |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0; Carry →1 |
Binary subtraction
When two binary numbers are subtracted, it gives rise to the binary subtraction.
Binary Numbers | Subtraction | |
0 | 0 | 0 |
0 | 1 | 1; Borrow 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Binary multiplication
The multiplication process for the binary number is the same. Here is an example –
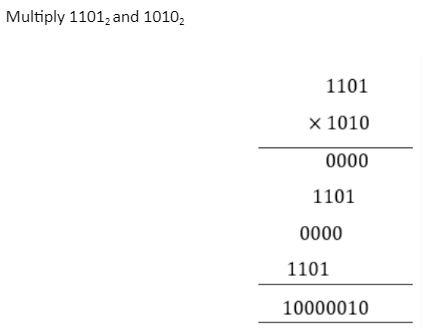
Binary division
The binary division is the same as the decimal number division method. Here is an example –

Conclusion
With this, we come to an end to the binary system of numbers. The binary system of numbers can be expressed as a number written in the base 2 numeral system or the binary system. It is one of the types of numbers in the number system.
In this article describing the binary system of numbers, we studied the concept of the number system and binary numbers in length. We covered several other topics, such as the binary system of numbers and other related topics. We hope this study material helped you better understand the binary system of numbers.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






