This easy-to-understand and well-written article focuses on analytical geometry, two-dimensional coordinate system and related terms, and two dimensions – equations of a line in various forms. Students will be made familiar with the concept of straight lines and related terms and formulas.
Depending on the type of information given, the equation for a straight line can be expressed in various forms: general form, Point slope form, Two-points form, Slope-Intercept form, Intercept form, and normal Perpendicular form.
Introduction to the Concept of Analytical Geometry
- Coordinate Geometry, also known as Analytical Geometry, is the field of mathematics that uses algebraic symbols and methods to represent and solve an equation for a problem in geometry.
- Analytical geometry establishes a correspondence between geometric curves and algebraic equations, making it possible to reformulate problems in geometry in terms of equivalent problems in algebra and vice versa.
Introduction to the Concept of Two-Dimensional Coordinate System
- In two-dimensional coordinate geometry, every point in two-dimensional space is assigned with unique coordinates that are used to identify the point in the plane or graph.
- Some important terms to be remembered are:
- Axes of Coordinates: The axes of coordinates are two intersecting straight lines used as reference lines in a graph or plane. A plane with X and Y axes and origin at O, OX and OY together form the axes of coordinates representing the X-axis and Y-axis, respectively.
- Origin and its Coordinate: The point of intersection of the X and Y axes is known as the origin of that plane and is denoted by ‘O’. The coordinate of an origin in a cartesian plane is (0, 0).
- Abscissa and Ordinate: The distance of any point on a plane from the Y-axis and X-axis is respectively known as abscissa and ordinate.
Introduction to Straight Lines and Related Terms
- A straight line is defined as a geometrical shape with no breadth and endpoints. It is extendable in both directions.
- In analytical geometry, a straight line is defined as the locus of a moving point P (h, k) such that the point P is always collinear with the two given fixed points, say A (x1, y1) and B (x2, y2).
- If a line cuts the x or y-axis at any point, then the abscissa or ordinate of that point is known as the x or y – Intercept of that line.
- The slope of a line, also known as gradient, is defined as the angle of inclination, say θ, made by the line with the positive X-axis in a 2D plane and is denoted by m.
- The slope is expressed as –
Slope = gradient = m = tan θ = (Perpendicular / Base) = /\Y / /\X = [(y2 – y1)/(x2 – x1)]. – eq. 1 (a)
Introduction to Two Dimensions – Eq. of a Line in Various Forms
- Depending on the type of information given, the equation for a straight line can be expressed in various forms such as general form, point slope form, two-points form, slope-intercept form, intercept form, and normal (or perpendicular) form.
- Two-points Form of Eq. of a Line: From the expressions obtained above, we can conclude that –
Slope (PA) = Slope (AB), i.e.,
[(y – y1)/(x – x1)] = [(y2 – y1)/(x2 – x1)]
- y – y1 = [(y2 – y1)/(x2 – x1)] (x – x1) — eq. 1 (b)
This is the equation of a straight line passing through two fixed points, A (x1, y1) and B (x2, y2).
- General Form of Eq. of a Line: On simplifying eq. 1 (b), we can express the equation as –
ax + by + c = 0, where a and b are the respective coefficients of x and y, and c is a constant.
Hence, ax + by + c = 0 is the general form of eq. of a line.
- Point Slope Form of Eq. of a Line: From the obtained expression of the slope of a line, eq. 1 (a) can be written as –
(y – y1) = m (x – x1), which is the required equation.
- Slope-Intercept Form of Eq. of a Line: Assuming ‘C’ is the y-intercept of a given line, the line with slope m will pass through the point with coordinates (0, C). Then, the equation of the line can be given by –
y – C = m (x – 0)
- y = mx + C, which is the required eq. of line.
- Intercept Form of Eq. of a Line: Assuming x and y-intercepts as A (a, 0) and B (0, b), then using eq. 1 (b), the new equation can be expressed as –
(y – 0) = [(b – 0)/(0 – a)] (x – a)
- (x/a) + (y/b) = 1, which is the required equation.
- Normal (or Perpendicular) Form of Eq. of a Line: Assume a line AB, whose distance from the centre perpendicularly is p and whose perpendicular OP forms an angle α with the horizontal x-axis.
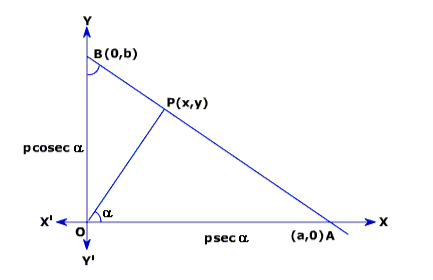
From the given figure, if / OPA = 90° and / POA = α, then / OBP is also equal to α. By using trigonometric formulas in right /\OPA, we have:
cos α = OP/OA
- OA = OP secα = p sec α.
Similarly, from right /\BPO, we have:
Sin α = OP/OB
- OB = OP cosec α = p cosec α.
Here, OA and OB are x and y-intercepts of line AB. Hence, by substituting their values in the intercept form, we get:
(x/p sec α) + (y/ p cosec α) = 1
- x cos α + y sin α = p, which is the required equation.
Conclusion:
The students have now understood the concepts of analytical geometry, two-dimensional coordinate system and related terms, and two dimensions – equations of a line in various forms.
They are now familiar with the concept of straight lines and related terms and formulas.
Two dimensions – equation of a line in various forms are – General form, Point slope form, Two-points form, Slope-Intercept form, Intercept form, and Normal (or Perpendicular) form.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






