This article aims to help students understand and grasp the concepts of analytical geometry, two-dimensional coordinate system, two dimensions – distance formula, and its derivation and applications.
The two dimensions – distance formula is a formula in analytical geometry to find the distance between two entities lying in a two-dimensional plane. These two entities could be two points, a point and a line, and two parallel lines.
The two dimensions – distance formula representing the distance (d) between any two points say, A (x1, y1) and B (x2, y2) in a Cartesian plane is expressed as –
d = √ [(x2 – x1)2 + (y2 – y1)2].
Introduction to the Concept of Analytical Geometry
- Coordinate Geometry, also known as Analytical Geometry, is the field of mathematics that uses algebraic symbols and methods to represent and solve an equation for a problem in geometry.
- Applications of Analytical geometry:
- Its concept is used in physics, engineering, aviation, rocketry, space science, and spaceflight.
- It provides the foundation for most modern geometrical fields such as – algebraic geometry, differential geometry, discrete geometry, and computational geometry.
- Analytical geometry establishes a correspondence between geometric curves and algebraic equations, making it possible to reformulate problems in geometry in terms of equivalent problems in algebra and vice versa.
Introduction to the Concept of Two-Dimensional Coordinate System
- In two-dimensional coordinate geometry, every point in two-dimensional space is assigned with unique coordinates used to identify the point in the plane or graph.
- Some important terms to be remembered are:
- Axes of Coordinates: The axes of coordinates are two intersecting straight lines used as reference lines in a graph or plane. A plane with X and Y axes and origin at O, OX and OY together form the axes of coordinates representing the X-axis and Y-axis, respectively.
- Origin and its Coordinate: The point of intersection of the X and Y axes is the origin of that plane and is denoted by ‘O’. The coordinate of an origin in a Cartesian plane is (0, 0).
- Abscissa and Ordinate: The distance of any point on a plane from the Y-axis and X-axis is respectively known as abscissa and ordinate.
- Quadrant: The X and Y axes divide the Cartesian plane into 4 equal parts known as quadrants. A quadrant is one-fourth of the plane divided by coordinate axes.
Introduction to Two Dimensions – Distance Formula, its Applications, and Derivation
Two Dimensions – Distance Formula Meaning and Importance
- Two dimensions – distance formula is a formula in analytical geometry to find the distance between two entities lying in a two-dimensional plane. These two entities could be two points, a point and a line, two parallel lines, etc.
- Distance between two points in 2D: Considering two points A (x1, y1) and B (x2, y2) on the Cartesian plane, the distance between them ‘d’, is given by the expression –
AB = d = √ [(x2 – x1)2 + (y2 – y1)2].
- Distance between a point and origin: Considering a point A (x, y) lying in a 2D plane. The distance from this point to the origin O (0, 0) is expressed as –
d = OA = √ (x2 + y2).
- Distance between a point and a line in 2D: Considering a point P (x1, y1) and a line L in a 2D plane, whose equation is ax + by + c = 0, the distance between them ‘d’, is given by the expression –
d = [|ax1 + by1 + c| / √ (a2 + b2)]
- Distance between two parallel lines in 2D: Since slopes of two parallel lines are the same, the distance between two parallel lines, L1 and L2, whose equations are axe + by +c1 and axe + by +c2 lying in the plane is given by –
d = [|c2 – c1] / √ (a2 + b2)].
Derivation of Two Dimensions – Distance Formula to Find the Distance Between Two Points
Consider two points, P (x1, y1) and Q (x2, y2), on the Cartesian plane. Draw PR and QS perpendicular to X-axis. Draw a perpendicular from the point P on QS, meet it at point T.
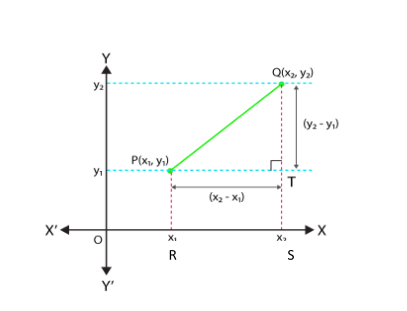
From the above figure, we can conclude that OR = x1, OS = x2, i.e., RS = PT = x2 – x1.
Similarly, SQ = y2, ST = PR = y1, i.e., QT = y2 – y1.
By applying Pythagoras theorem in /\ PTQ, we have:
PQ2 = PT2 + QT2
= (x2 – x1)2 + (y2 – y1)2
Hence, PQ = √ [(x2 – x1)2 + (y2 – y1)2]; we only consider the positive square root since distance is always positive.
We can now conclude that, the distance between two points P (x1, y1) and Q (x2, y2) is given by –
d = PQ = √ [(x2 – x1)2 + (y2 – y1)2]; which is the distance formula.
Applications of Two Dimensions – Distance Formula
- Calculating the distance of any point from the origin.
- The formula to find the magnitude of a complex number can be derived from the distance formula.
- It is used to calculate the distance between two points, a point and a line, and two parallel lines lying in a two-dimensional plane.
- It is used to find the magnitude of a vector quantity.
- The distance formula can calculate the shortest distance between two places by air.
Conclusion:
Through this article on Analytical Geometry – Two dimensions – distance formula – Maths, students can understand and grasp the concepts of analytical or coordinate geometry and its applications, two-dimensional (or 2-D) coordinate system, as well as two dimensions – distance formula and its derivation and applications.
We have also learnt that the two dimensions – distance formula is a formula in analytical geometry to find the distance between two entities lying in a two-dimensional plane.
Students now know the two dimensions – the distance formula for calculating the distance between two points, a point and a line, and two parallel lines lying in a two-dimensional plane.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






