Profile
Settings
Refer your friends
Sign out
Set is nothing but the collection of elements or functionalities which can be grouped together. They can be either mathematical or not. Set is usually represented pictorially in terms of Venn diagrams. These are grouped using flower brackets{}. Operations of sets are usually done. These operations of sets are almost similar to the operations of natural numbers. Natural numbers have properties between them. Same as those properties of natural numbers sets also have the properties like that.
Operations of sets:
The following are the operations of sets:
1) Intersection on sets
2) Union on sets
3) Compliment on sets
4) Difference on sets
5) Cartesian Product
Similar to the natural numbers the set operations also have the above properties. Operations of sets can also be done in roaster form.
In roaster form, the natural numbers are used to represent the sets.
Operations of the set – Intersection of sets
The intersection of sets in roaster form.
Let’s consider an example:
1) Set A={2, 4,5,8,10,6}, Set B={1, 2,4,10,5,7}.Find the intersection of A And B.
Solution : A∩B={2, 4, 5,10}
2) Find the Intersection of sets for the following sets.
A={a, e, i,o, u}, B= {p, q, r, w}
Solution: A ∩ B =ϕ
The intersection of sets is picking up the same elements in the two sets. Here. in example two there are no same elements hence the answer is a null value which is ϕ.
Some of the things that we need to keep in mind when we deal with the intersection of sets.
- A ∩ B =B ∩ A
- A ∩ A =A
- Φ ∩ A = A
The general expression that is used for finding the intersection on sets is.
A ∩ B = A + B – A ∪ B
Some of the properties on the intersection of sets:
- A ∩ A= A
- A ∩ ϕ = ϕ
- ϕ ∩ ϕ = ϕ
The above properties and formulae of the intersection of sets are Applicable for the probability too.
When discussing the operations of sets we come across the probability topic too.
When discussing the operations of sets we come across represented through Venn diagrams.
The pictorial representation of A ∩B is as follows:
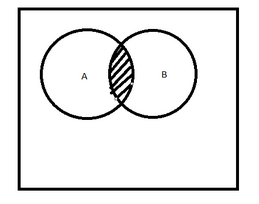
The highlighted area shows the intersection which means the common points or common elements in the three, two sets.
Along with the above properties. If the A, B are the disjoint sets. The P( A ∩B) = P(A) x P(B) where both are independent of each other and both events happen together.
If A and B are mutually exclusive the P(A ∩B) = 0
We also have P( A∩B) = P(A). P(B/A) if event A occurs after event B.
Along with the intersection of sets, the sets also exhibit the following operations.
Union of sets:
Union of the sets is nothing but the combination of both sets that means all the elements that are present in A, B as well as both. Natural numbers are used mathematically.
Let’s Consider an example:
Example 1: Set A= {1, 2,4} , Set B = { 1,5,6}
Here A ∪B is A ∪ B= {1, 2,4,5,6}
Example 2: Set A = { 1,2,5}, Set B = {}
Here A ∪ B = { 1,2,5}
The difference is also one of the Operations of sets
Venn diagram highlights the difference part:
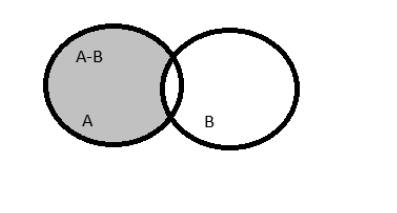
Here A-B represents the elements only in A not in B.
Example 1: Set A= { 1,2,3,4} , B = { 1,2,4}
A – B is { 3}
The natural numbers are taken, for example, generally, these operations are done both mathematically and non- mathematically.
Complement on sets:
Consider a union set and a normal set ,substrating the A from the union gives the compliment set.
Considering set U = { 1,2,3,4,7,9,10} A = { 2,3,4}
A compliment Ac = U – A
{1, 7,9,10}
Cartesian product :
Cartesian product is also an interesting operation on sets which has natural number operations, these sets are the order pairs. It represents the whole set of combinations among the sets involved.
For example, consider two sets.
Example 1: A= { 1,2} and B={3, 4}
The Cartesian product of the above two sets is {(1, 3), (1, 4), (2, 3), (2, 4) }
Conclusion:
Hence we can conclude that the sets also satisfy the properties of the natural numbers. Along with that, the intersection operation is the major operation for the sets with various properties. These sets also satisfy the probability concepts. Majorly, the sets are used to represent a large amount of data. Various concepts using the pictorial representation of Venn diagrams can be understood easily. The intersection on sets along with the Union is used to solve many concepts in mathematics which are critical.
