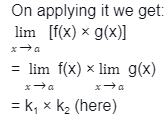Profile
Settings
Refer your friends
Sign out
Algebraic operations on continuous functions involve different rules that deal with their application in algebraic equations involving various binary operations. As the name states, a continuous function is a type of function with a continuous graph, i.e., one without any break or jumps. We can draw these types of graphs without lifting our pencils. A continuous function is a very important aspect of calculus as only a continuous function is differentiable. If there is a little break or jump in the graph, the function is said to be non-continuous. All polynomial functions on the set of real numbers are continuous. The absolute value for |x| and exponential functions are continuous at real numbers. Let’ us study the Algebraic operations on continuous functions and their rules in brief.
Addition of two continuous functions
f + g: continuous at x = x0,
Subtraction of two continuous functions:
f – g: continuous at x = x0
Proof of addition and subtraction of two continuous functions:
To prove the continuity of (f(x) + g(x)) at x = a, we have to verify for three different conditions. As we know, f(x) and g(x) are continued functions (at x=a),
We know that f(a) and g(a) are defined
Assume,xaf(x) = f(a) = k1 and xag(x) = g (a) = k2
We get by using them:
= [f(a) + g(a)] is clearly defined at x = a {as both f(a) and g(a) are defined}.
= According to the Summation Law of limits that says that the limit of a sum is always equal to the sum of the limits, we get:
xa [f(x) + g(x)]
= xaf(x) + xag(x)
= k1 + k2 (here)
=> f(a) + g(a) = k1 + k2 = xa[f(x) + g(x)]
Therefore, we can conclude that the function [f(x) + g(x)] is continuous at x = a. (for the subtraction rule, we just need to replace signs of addition ‘+’ by subtraction ‘-‘)
Multiplication rules
f(x)×g(x): continuous at x = a
Proof of multiplication rules of two continuous functions
We can prove the multiplication rule by using the merchandise Law of limits.
The merchandise law of limit states that the limit of a product is the product of the limits.
On applying it we get:
xa [f(x) × g(x)]
= xa f(x) × xa g(x)
= k1 × k2 (here)
Division rules
f(x)/g(x): continuous at x = a
and g(a) ≠0
Proof of division rules of two continuous functions
We can prove the division rule by using the Quotient Law of limit.
The quotient law of limits states that the limit of a quotient is the quotient of the limit.
On applying it we will get:
xa [f(x)/g(x)]
= xa f(x)/xa g(x)
= k1/k2 (here, given k2 ≠ 0)
Composite rule
f(g(x)) and g(f(x)): continuous at x = a
Solved questions on Algebraic operations on continuous functions
Q 1- Determine if the function f(x) = sin(x3 + 5) is continuous (at x = 0)?
Solution:
By looking at the question, we can say that this function is the composition of two continuous functions:
g1(x) = sin x and
g2(x) = (x3 + 5)
f(x)=g1[g2(x)]
Thus, by the composition rule as stated above,
f(x) is continuous at x = 0.
Q 2- A function is given as f(x) = 3x – 7. Find whether it is a continuous function at x = 7.
Solution:
According to the question,
f(x) = 3x – 7, where x = 7 (a)
Finding thexaf(x) and f(a).
xaf(x)
=x7 (3x – 7)
= 3(7) – 7
= 21 – 7
= 14.
f(a) = f(7)
= 3(7) – 7
= 21 – 7
= 14.
So we can conclude that,xaf(x) = f(a).
Therefore, f(x) = 3x – 7 is continuous at x = 7.
Conclusion
Algebraic Operations on Continuous Functions are the functions that deal with the application of continuous functions in the algebraic equation that involves various binary operations. As the name says, a continuous function is a type of function with a continuous graph without any break or jumps. We can draw these types of graphs without lifting up our pencils. A continuous function is a very important aspect of calculus as only a continuous function is differentiable. All polynomial functions on the set of real numbers are continuous. The absolute value for |x| and exponential functions are continuous at real numbers. There are rules for addition, subtraction, multiplication, and division for a continued fraction as stated above.
