Introduction
Matrix is a collection of elements in rows and columns form. It is used to operate the elements according to requirements. Matrix is an important concept in high-level maths and other fields like computer science, master’s programs, etc. Transpose of a matrix, multiplication of matrix, the inverse of the matrix is some concepts.
The determinant is used to determine the square matrix as a single value for analysing purposes. The determinant method is used to obtain the scalar value of the square matrix.
In this article, we will discuss- expanding matrices by column
- expand pam matrices used in bioinformatics
- can matrices be Taylor expanded?
These are some major topics covered in this article.
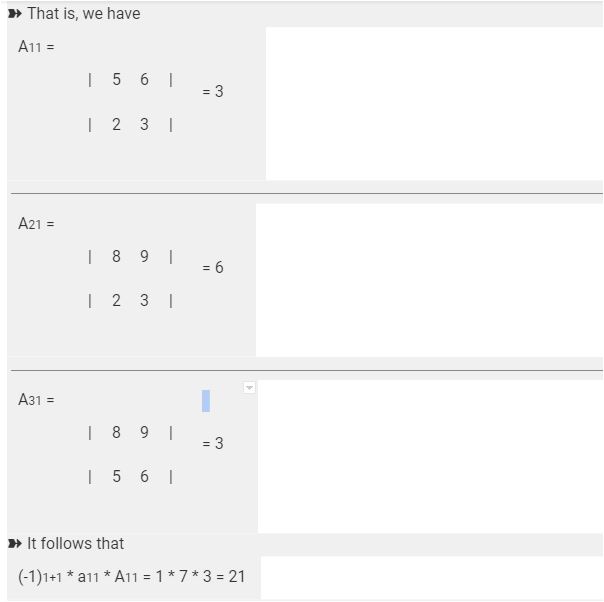
Expanding matrices by column to find the determinant
We can find the determinant by expanding matrices by column. We can take any column, but the first column is usually preferred to avoid mistakes. Hence, here we will try to expand through the first column. You will have two notations, i and j. In matrices, I represents rows, and j represents columns. Hence, instead of these notations, we can write numbers also to address an element. Expanding matrices is a huge task itself, and one should be careful with positive and negative signs of numbers for calculation correctness.
The formula for expanding matrices by column –
det(A) = (-1)i+1 * ai1 * det(Ai1) + (-1)i+2 * ai2 * det(Ai2) + … + (-1)i+n * ain * det(Ain).
Note –
- Sign of the operand changes as follows: pattern -,+,-,+,-,+, and so on.
- Det stands for determinant. The symbol of the determinant is det().
- This method is also called cofactors of matrices. This term is widely used in matrices.
- You should practice the formula and solve the fundamental question, as silly mistakes in calculation will ultimately lead you to the wrong answer.
Steps for expanding matrices by column –
- Select the first element of the first column.
- Selected element rows and columns are not considered for calculating determinants.
- Calculate the determinant of remaining elements by the determinant method.
- Do the same for all remaining elements of the first column.
- Finally, add all determinants, and you will get the solution.
Go through the following examples for a clear understanding.




Expand pam matrices used in bioinformatics
Now, let us move towards another topic that is expanding PAM matrices used in bioinformatics. Before we proceed further, we should understand, What is PAM?
The full form of PAM is Point Accepted Mutation. This term is used in finding and substituting the mutation in amino acids. Amino acids are presented in the primary structure of proteins. PAM matrix helps us to note down the mutations and substitute them with other amino acids.
PAM matrices consist of rows and columns with the encoding of amino acids. There are different types of PAM matrices like PAM20, PAM100, etc. But, PAM 250 is the most common PAM matrix used nowadays.
The main use of PAM matrices is finding mutations, which helps us track our ancestors. We can track our ancestors by finding out the mutations in fossils. Expand PAM matrices used in bioinformatics done by probability method. Using probability techniques, the matrix is created according to the PAM number and scaling factor.
Taylor Series
Now, let’s discuss whether matrices can be Taylor expanded. If I can give a short answer, then it is yes. Matrices can be Taylor expanded. Now, understand this in detail.
Taylor is a series that is taught in high-level mathematics. This series is used in the computer science field, calculus, and different science streams like physics and chemistry. This series tells us how the differentiation of the function looks on cartesian product graphs.
Functions can be trigonometric, algebraic, etc. The Cartesian graph is represented as the x and y-axis. Hence, we can consider these two axes as rows and columns, and we know that the matrix consists of rows and columns. We can expand this matrix through the functions.
Hence, the question asked as matrices can be Taylor expanded is answered as yes. There are many formulas on the Taylor series as the differentiation function is defined. Hence. You can understand differentiation also to move further on the Taylor series.
Conclusion
In this article, we learned about matrix expansion with examples. We discussed cofactors in this article. Also, steps point to be noted, and some examples of expanding matrices by column are given.
Also, we discussed expanding pam matrices used in bioinformatics. What is PAM, where are they used, how to expand them are the topics discussed in this section.
Then came across the Taylor series. Also, we tried to answer the question – can matrices be Taylor expanded in brief. Also, we discussed the use of the Taylor series and how to convert them into matrix form. Hope you understand the expansion of the matrix, enjoy learning!
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






