NCERT Solutions Class 9 Maths Chapter 8- Quadrilaterals

Exercise – 8.1

Q.1. The angles of the quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral.
Solution:
Let us consider the common ratio between the angles be=x
And we know that the sum of the interior angles of quadrilateral is= 360^{0} Now, 3x+5x+9x+13x=360^\circ \\ 30x=360^{\circ}\\ x=12^{\circ}\\ \text{Angles of the Quadrilateral are:}\\ 3x=3\times 12^{\circ}=36^{\circ}\\ 5x=5\times 12^{\circ}=60^{\circ}\\ 9x=9\times 12^{\circ}=108^{\circ}\\ 13x=13\times 12^{\circ}=156^{\circ}\\

Q.2. If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Answer:

According to the question,
AC=BD
To show that, ABCD is a rectangle if the Diagonals of a Parallelogram are Equal.
Now, to show ABCD is a rectangle we have to prove that one of its interior angles is right angled.
Proof:
In \triangle ABC \text{ and } \triangle BAD
AB=BA(Common)
BC=AD (Opposite Sides of A Parallelogram are equal)
AC=BD(Given)
Therefore, \triangle ABC\cong \triangle BAD [SSS Congruency]
\angle A=\angle B [Corresponding parts of Congruent Triangles
Also,
\angle A+\angle B=180^{0}\\ 2\angle A=180^{0}\\ \angle A=90^{0}=\angle B\\
Therefore, ABCD is a Rectangle
Hence Proved.

Q.3. Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
Answer:

Let ABCD be a Quadrilateral whose Diagonals bisect each other at right angles.
Given in the Question,
OA=OC
OB=OD
And \angle AOB=\angle BOC=\angle OCD=\angle ODA=90^{0}
To Show,
If the Diagonals of a Quadrilateral bisect each other at right angles, then it is a Rhombus. Hence, we have to Prove that ABCD is Parallelogram and AB=BC=CD=AD.
\text{In } \triangle AOB \text{ and } \triangle COB
OA=OC [Given]
\angle AOB=\angle COB (Opposite sides of a Parallelogram are Equal)
OB=OB[Common]
Therefore, \triangle AOB\cong \triangle COB [SAS Congruency]
Thus, AB=BC [CPCT]
Thus, we can prove that,
BC=CD
CD=AD
AD=AB
AB=BC=CD=AD
Opposite Sides of a Quadrilateral are equal hence ABCD is a Parallelogram.
Hence, ABCD is rhombus as it is a Parallelogram whose diagonals intersect at right angle.
Hence Proved.
Q.4. Show that the diagonals of a square are equal and bisect each other at right angles.
Answer:

Let us consider ABCD be a Square and its diagonals AC and BD intersect each other at O.
To Show that,
AC=BD
AO=OC
and \angle AOB=90^{0}
Proof:
\text{In } \triangle ABC \text{ and } \triangle BAD,
BC=BA[Common]
\angle ABC=\angle BAD=90^{0}
AC=AD[Given]
Therefore \triangle ABC \cong \triangle BAD [SAS Congruency]\\
Thus,
AC=BD [CPCT]
diagonals are equal.
Now,
\text{In } \triangle AOB \text{ and } \triangle COD,\\ \angle BAO=\angle DCO \text{ (Alternate interior Angles) }\\ \angle AOB= \angle COD \text{ (Vertically Opposite) }\\ AB=CD \text{ [Given] }\\ \triangle AOB \cong \triangle COD \text{ [AAS Congruency] }
Thus,
AO=CO[CPCT]
Diagonal bisect each other.
Now,
\text{In } \triangle AOB \text{ and } \triangle COB,\\ OB=OB \text{ [Given] }\\ AO=CO \text{ [Diagonals are Bisected] }\\ AB=CB \text{ [Sides of the Square] }
Hence,
\triangle AOB \cong \triangle COB \text{ [SSS Congruency] }\\ \text{Also, } \angle AOB=\angle COB\\ \angle AOB + \angle COB=180^{0}\\ \text{Thus, } \angle AOB=\angle COB=90^{0}
Hence, Diagonal bisect each other at right Angles.

Q.5. Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
Answer:
Given in the Question,
Let us Consider ABCD to be a Quadrilateral and its diagonal AC and BD bisect each other at right angle at O.
To Prove,
The Quadrilateral ABCD is a Square.
Proof:
\text{In } \triangle AOB \text{ and } \triangle COD,\\ AO=CO 9 \text{ [Diagonal bisect each other] }\\ \angle AOB =\angle COD \text{ [Vertically Opposite] }\\ OB=OD \text{ [Diagonal bisect each other] }\\ \text{Hence, } \triangle AOB \cong \triangle COD \text{ [SAS Congruency] }
Thus,
AB=CD [CPCT]\to (i)\\ \text{Also, }\\ \angle OAB =\angle OCD \text{ [Alternate interior Angle] }\\ AB||CD\\ \text{Now,} \\ \text{In } \triangle AOD \text{ and } \triangle COD,\\ AO=CO \text{ [Diagonals Bisect each other] }\\ \angle AOD=\angle COD \text{ [Vertically Opposite] }\\ OD=OD \text{ [Common] }\\ \text{Hence, } \triangle AOD \cong \triangle COD \text{ [SAS Congruency] }\\ \text{Thus, }\\ AD=CD \text{ [CPCT] }\\ \text{Also, }\\ AD=BC \text{ and } AD=CD\\ \text{Also, } AD=BC=CD=AB \to (iii)\\ \text{Also,}\\ \angle ADC=\angle BCD \text{ [CPCT] }\\ \text{And } \angle ADC + \angle BCD=180^{0}\\ 2\angle ADC=180^{0}\\ \angle ADC=90^{0}\to (iv)
Hence, one of the Interior Angle is Right angle.
Thus From (i), (ii) and (iii) given Quadrilateral ABCD is a Square.
Hence Proved.

Q.6. Diagonal AC of a parallelogram ABCD bisects ∠ A (see Fig. 8.19). Show that
(i) it bisects ∠ C also,
(ii) ABCD is a rhombus.

Solution:

(i) \text{In } \triangle ADC \text{ and } \triangle CBA\\, AD=CB \text{ [Opposite sides of a Parallelogram] }\\ DC=BA \text{ [Opposite Sides of a Parallelogram] }\\ AC=CA \text{ [Common Side] }\\ \text{Hence, }\triangle ADC \cong \triangle CBA \text{ [SSS Congruency] }\\ \text{Thus, } \angle ACD=\angle CAB \text{ by CPCT }\\ \text{And } \angle CAB= \angle CAD \text{ [Given] }\\ \angle ACD=\angle BCA\\ \text{Thus, } AC \text{ bisect } \angle C \text{ also. }
(ii) \angle ACD =\angle CAD \text{ [proved Above] }\\ AD=CD \text{ [Opposite sides of a equal angle of a triangle are equal] }\\ AB=BC=CD=DA \text{ [Opposite Sides of a Parallelogram] }
Thus, ABCD IS Rhombus.
Q.7. ABCD is a rhombus. Show that diagonal AC bisects ∠ A as well as ∠ C and diagonal BD, bisects ∠ B as well as ∠ D.
Answer:

Given That in the Question
ABCD is a Rhombus.
AC and BD are its Diagonals.
Proof.
AD=CD \text{ [Sides of a rhombus] }\\ \angle DAC=\angle DCA \text{ [Angles opposite of equal sides of a Triangle are Equal] }\\ \text{Also, }\\ AB||CD\\ \angle DAC=\angle BCA \text{ [Alternate Interior Angle] }\\ \Rightarrow \angle DAC=\angle BCA\\ \text{Hence, } AC \text{ bisects } \angle C.\\ \text{Similarly}
We can prove that Diagonal Bisects.
Hence Proved.

Q.8. ABCD is a rectangle in which diagonal AC bisects ∠ A as well as ∠ C. Show that:
(i) ABCD is a square (ii) diagonal BD bisects ∠ B as well as ∠ D.
Answer:

(i) \angle DAC =\angle DCA\\ AD= CD \text{ [Sides opposite to equal angles of a triangle are equal] }\\ \text{Also, } CD=AB \text{ [Opposite Sides of a Rectangle] }\\ \text{Hence, } AB=BC=CD=AD\\ \text{Thus, ABCD is a Square }
(ii) \text{In }\triangle BCD\\ BC=CD\\ \angle CDB =\angle CBD \text{ [Angles opposite to equal sides are Equal] }\\ \text{Also, }\angle CDB=\angle ABD \text{ [Alternate interior Angle] }\\ \angle CBD=\angle ABD\\ \text{Thus, } BD \text{ bisects } \angle B\\ \text{Now, }\angle CBD= \angle ADB\\ \angle CDB =\angle ADB\\ \text{Thus, }BD \text{ bisects }\angle B \text{ as well as } \angle D.

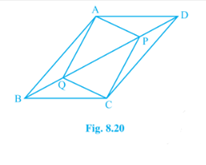
Q.9. In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ (see Fig. 8.20). Show that:
(i) ∆ APD ≅ ∆ CQB
(ii) AP = CQ
(iii) ∆ AQB ≅∆ CPD
(iv) AQ = CP
(v) APCQ is a parallelogram

Answer:

(i) \text{In }\triangle APD \text{ and }\triangle CQB,\\ DP=BQ \text{ [Given] }\\ \angle ADP=\angle CBQ \text{ [Alternate Interior Angle] }\\ AD=BC\\ \text{Thus, }\triangle APD\cong \triangle CQB \text{ [SAS Congruency] }
(ii) AP=CQ \text{ by CPCT as }\triangle APD \cong \triangle CQB.
(iii) \text{In }\triangle AQB \text{ and } \triangle CPD,\\ BQ=DP \text{ [Given]} \\ \angle ABQ= \angle CDP \text{ [Alternate Interior Angle] }\\ AB=CD\\ \text{Thus, }\triangle AQB\cong \triangle CPD \text{ [SAS Congruency] }
(iv) \text{As }\triangle AQB \cong \triangle CPD\\ AQ=CP \text{ [CPCT] }
(v) From (ii) and (iv) it is clear that APCQ has equal opposite sides and also has equal and opposite Angles.
Hence, APCQ is a Parallelogram.

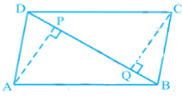
Q.10. ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal
BD (see Figure). Show that
(i) ∆ APB ≅ ∆ CQD
(ii) AP = CQ

Answer:

(i) \text{In } \triangle APB \text{ and }\triangle CQD,\\ \angle ABP=\angle CDQ \text{ [Alternate interior Angles] }\\ \angle APB =\angle CQD=90^{0} \text{ [as AP and CQ are Perpendiculars] }\\ AB=CD \text{ [ABCD is a Parallelogram] }\\ \text{Hence, }\triangle APB \cong \triangle CQA \text{ [AAS Congruency] }

(ii) \text{As }\triangle APB \cong \triangle CQD\\ \text{Therefore, }AP=CQ \text{ [CPCT] }

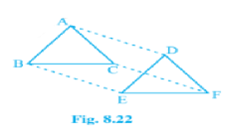
Q.11. In ∆ ABC and ∆ DEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, B and C are joined to
vertices D, E and F respectively (see Fig. 8.22).
Show that
(i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ∆ ABC ≅ ∆ DEF.

Solution:

AB=DE and AB||DE [Given]
Two opposite sides of a Quadrilateral are the same and parallel to each other.
Thus, Quadrilateral ABED is a Parallelogram.
Again BC=EF and BC||EF.
Thus, Quadrilateral BECF is Parallelogram.
Since ABED and BEFC are Parallelogram.
AD=BE and BE=CF [Opposite sides of a Parallelogram are Same]
Hence, AD=CF.
Also, AD||BE and BE||CF (Opposite Sides of a Parallelogram are Parallel)
AD and CF are Opposite sides of Quadrilateral ACFD which are Same and Parallel to each Other. Thus it is a Parallelogram.
Since ACFD is a Parallelogram
AC||DF and AC=DF.

(vi) \text{In }\triangle ABC \text{ and }\triangle DEF,\\ AB=DE \text{ [Given] }\\ BC=EF \text{ [Given] }\\ AC=DF \text{ [Opposite sides of a Parallelogram] }\\ \text{Hence, }\triangle ABC \cong \triangle DEF \text{ [SSS Congruency] }

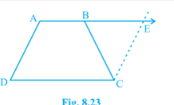
Q.12. ABCD is a trapezium in which AB || CD and
AD = BC (see Fig. 8.23). Show that
(i) ∠ A = ∠ B
(ii) ∠ C = ∠ D
(iii) ∆ ABC ≅ ∆ BAD
(iv) diagonal AC = diagonal BD
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]

Solution:

To Construct: Draw a line through C Parallel to DA intersecting AB Produce at E.
(i) CE=AD \text{ [Opposite sides of a Parallelogram] } \\ AD=BC \text{ [Given] }\\ BC=CE\\ \angle CBE = \angle CEB\\ \text{Also, } \angle A + \angle CBE=180^{0}\\ \angle B+\angle CBE=180^{0} \text{ [As Linear pair] }
(ii) \angle A +\angle D = \angle B+\angle C=180^{0}\\ \angle A+\angle D=\angle A+\angle C (\angle A=\angle B)\\ \angle D=\angle C
(iii) \text{In }\triangle ABC \text{ and } \triangle BAD,\\ AB=AB \text{ [Common] }\\ \angle DAB=\angle CBA\\ AD=BC \text{ (Given) }\\ \text{Therefore, }\triangle ABC \cong \triangle BAD \text{ [SAS Congruency] }
(iv) \text{Diagonal AC } = \text{ Diagonal BD by CPCT as }\triangle ABC \cong \triangle BAD.

Exercise 8.2

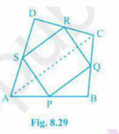
Q.1. ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA
(see Fig 8.29). AC is a diagonal. Show that :
(i) SR || AC and SR=1/2 AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.

Solution:

(i) \text{In }\triangle DAC,\\ \text{R is the mid-point of DC and S is the mid-point of DA.}\\ \text{Thus, by mid-point theorem, SR||AC and }SR=\frac{1}{2}AC.
(ii) \text{In }\triangle BAC,\\ \text{P is the mid-point of AB and Q is the Mid-point of BC. }\\ \text{Thus, by mid-point theorem, PQ||AC and } PQ=\frac{1}{2} AC\\ \text{Therefore, }PQ=SR

(iii) SR||AC \rightarrow \text{ from question (i) }\\ \text{And }PQ||AC\rightarrow \text{ from question (ii) }\\ \text{Hence, SR||PQ-from (i) and (ii)}\\ \text{Also, } PQ=SR\\ \text{Hence, PQRS is a Parallelogram. }

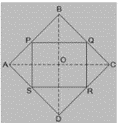
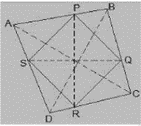
Q.2. ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
Solution:

Given in the Question,
ABCD is a Rhombus and P,Q,R and S are the mid-points for the sides AB,BC,CD and DA Respectively.
To Prove,
PQRS is a Rectangle.
Construction,
Join AC and BD.
Proof:
\text{In }\triangle DRS \text{ and } \triangle BPQ,\\ DS=BQ \text{ (Halves of the opposite side of the Rhombus) }\\ \angle SDR=\angle QBP \text{ (Opposite angles of the Rhombus)}\\ DR=BP\\ \text{Hence, }\triangle DRS \cong \triangle BPQ, \text{ [SAS Congruency] }\\ RS=PQ \text{ [CPCT] }\rightarrow (i)\\ \text{In } \triangle QCR \text{ and } \triangle SAP,\\ RC=PA \text{ (Halves of the opposite sides of the rhombus) }\\ \angle RCQ= \angle PAS \text{ (Opposite angles of the rhombus) }\\ CQ=AS\\ \text{Hence, }\triangle QCR \cong \triangle SAP \text{ [SAS Congruency }\\ RQ=SP [CPCT]\rightarrow (ii)\\ \text{Now, }\\ \text{In }\triangle CDB,\\ \text{R and Q are the mid-points of CD and BC respectively. }\\ \text{Hence,} QR||BD\\ \text{Also, }\\ \text{Given that P and S are the mid-points of AD and AB respectively.}\\ PS||BD\\ QR||PS\\ \text{Hence, PQRS is a Parallelogram.}\\ \text{Also, } \angle PQR=90^{0}\\ \text{Now, }\\ \text{In PQRS,}\\ \text{RS=PQ and RQ=SP from (i) and (ii) }\\ \angle Q=90^{0}\\ \text{Hence, PQRS is a Rectangle. }

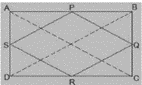
Q.3. ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
Answer

Given that,
ABCD is a rectangle and P,Q,R and S are the mid-points of the sides AB,BC,CD and DA respectively.
Construction
Join AC and BD.
To Prove,
PQRS is a rhombus.
Proof:
\text{In }\triangle ABC \text{P and Q are the Mid-points of AB and BC respectively. }\\ PQ||AC and PQ=\frac{1}{2}AC \text{ (Midpoint Theorem) }\rightarrow (i)\\ \text{In } \triangle ADC,\\ SR||AC \text{ and } SR=\frac{1}{2}AC \text{ (Midpoint Theorem) }\rightarrow (ii)\\ \text{So, } PQ||SR \text{ and } PQ=SR\\ \text{ AS in Quadrilateral PQRS one pair of Opposite sides is equal and parallel to each other, so it is a parallelogram.}\\ \text{Therefore PS||QR and PS=QR (Opposite sides of Parallelogram) }\rightarrow (iii)\\ \text{Now, }\\ \text{In } \triangle BCD,\\ \text{Q and R are the Mid-points of side BC and CD respectively. }\\ QR||BD \text{ and } QR||\frac{1}{2}BD \text{ (Mid-point Theorem) }\rightarrow (iv)\\ AC=BD \text{ (Diagonals of a rectangle are equal) }\rightarrow (v)\\ \text{ Now from equation (i),(ii),(iii),(iv) and (v), } \\ PQ=QR=SR=PS\\ \text{Hence, PQRS is Rhombus.}\\ \text{Hence Proved }

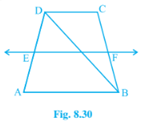
Q.4. ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see Fig. 8.30). Show that F is the mid-point of BC.

Solution:

Given That,
ABCD is a Trapezium in which AB||DC, BD is a Diagonal and E is the mid-point of AD.
To Prove,
F is the Mid-point of BC.
Proof,
\text{BD intersected EF at G.}\\ \text{In }\triangle BAD,\\ \text{E is the mid-point of AD and also EG||AB.}\\ \text{Thus, G is the mid-point of BD (Converse of mid-point theorem)}\\ \text{Now, }\\ \text{In } \triangle BDC,\\ \text {G is the mid-point of BD and also GF||AB||DC. }\\ \text{ Thus, F is the mid-point of BC (Converse of mid-point Theorem) }

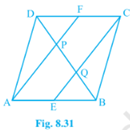
Q.5. In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see Fig. 8.31). Show that the line segments AF and EC trisect the diagonal BD.

Solution:

Given that,
ABCD is a Parallelogram. E and F are the mid-points of Sides AB and CD respectively.
To Show,
AF and EC trisect the Diagonal BD.
Proof,
ABCD is a Parallelogram.
Hence, AB||CD
Also, AE||FC
Now,
AB=CD \text{ (Opposite Sides of Parallelogram ABCD) }\\ \frac{1}{2} AB=\frac{1}{2} CD\\ AE=FC\\ \text{AECF is a Parallelogram (AE and CF are parallel and equal to each other) }\\ \text{AF||EC (Opposite sides of a parallelogram)}\\ \text{Now, }\\ \text{In }\triangle DQC,\\ \text{F is mid point of side DC and FP||CQ}\\ \text{P is the mid-point of DQ }\\ DP=PQ\rightarrow (i)\\ \text{Similarly, }\\ \text{In }\triangle APB,\\ \text{E is mid-point of side AB and EQ||AP.}\\ \text{ Q is the mid-point of PB(Converse of mid-point theorem)}\\ PQ=QB\rightarrow (ii)\\ \text{ From equation (i) and (ii) }\\ DP=PQ=BQ\\ \text{Hence, the line segments AF and EC trisect the Diagonal BD.}

Q.6. Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
Solution:

Let us Consider ABCD be a Quadrilateral and P,Q,R and S are the mid-points of AB, BC,CD and DA respectively.
Now,
\text{In }\triangle ACD,\\ \text{ R and S are the points of CD and DA Respectively.}\\ \text{Hence, }SR||AC,\\ \text{Similarly we can show that}\\ PQ||AC,\\ PS||BD \text{ and }\\ QR||BD\\ \text{Hence, PQRS is a Parallelogram.}\\ \text{PR and QS are the diagonals of the parallelogram PQRS. So, they will bisect each other.}

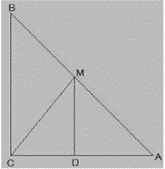
Q.7. ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC (ii) MD ⊥AC
(iii) CM = MA =1/2 AB.
Solution:

\text{In }\triangle ACB,\\ \text{M is the mid-point of AB and MD||BC}\\ \text{D is the mid-point of AC. (Converse of Mid-point Theorem)}

(ii) \angle ACB= \angle ADM \text{ (Corresponding Angles) }\\ \text{Also }\angle ACB=90^{0}\\ \text{Hence, }\angle ADM=90^{0} and MD \perp AC

(iii) \text{In }\triangle AMD \text{ and }\triangle CMD,\\ AD=CD \text{ (D is the mid point of AC) }\\ \angle ADM=\angle CDM (Each 90^{0})\\ DM=DM \text{ (Common) }\\ \text{Hence, }\triangle AMD\cong \triangle CMD \text{ [SAS Congruency] }\\ AM=CM \text{ [CPCT] }\\ \text{Also, }AM=\frac{1}{2} AB \text{ (M is the mid-point of Side AB) }\\ \text{Hence, }CM=MA=\frac{1}{2}AB.