NCERT Solutions for Class 9 Maths Chapter 7 Triangles includes answers and questions from the chapter, which is part of the CBSE Term I Syllabus. The word triangle describes its meaning. A Triangle is a closed figure formed by three intersecting lines. “Tri” means “three.” NCERT Class 9 Maths Chapter 6 should have covered the angle sum property of a triangle. In addition, Chapter 7 of NCERT Solutions for Class 9 Maths will teach students about triangle congruence and congruence rules. They will also be taught some more triangle properties and inequalities.
We have provided the entire Class 9 Maths NCERT Solutions Chapter 7 Triangles in PDF format, which were solved by experienced teachers. By clicking on the link below, students can save the free PDF of these NCERT Solutions for Class 9 for future reference.
NCERT Solutions for Class 9 Maths - Triangles PDF preview
Exercise 7.1
Q1. In quadrilateral ACBD, AC = AD and AB bisect \angle A (see Fig. 7.16). Show that \mathrm{\Delta ABC}\cong\ \mathrm{\Delta ABD} . What can you say about BC 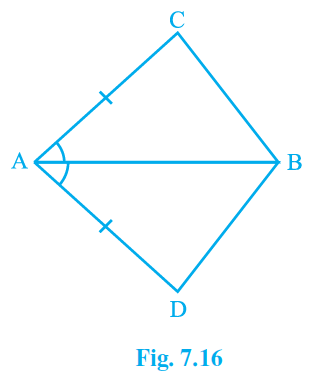 and BD?
and BD?
Answer:
AC and AD are given to be equal, i.e. AC = AD, and the line segment AB bisects the angle A.
We must now show that the two triangles ABC and ABD are equivalent, i.e. \mathrm{\Delta ABC}\cong\ \mathrm{\Delta ABD} .
Proof: we will be considering \mathrm{\Delta ABC}\ and\ \mathrm{\Delta ABD} ,
AC = AD (already mentioned in the question)
AB = AB (Common for both the triangles)
\angle ABC\cong\angle ABD (Since AB is bisecting angle A)
As a result of the SAS congruency criteria, \mathrm{\Delta ABC}\cong\ \mathrm{\Delta ABD} .
By the C.P.C.T. criterion, BC and BD are of equal length in the second portion of the question.
Q2. ABCD is a quadrilateral in which AD = BC and \angle DAB\ =\ \angle CBA (see Fig. 7.17). Prove that
(i) \mathrm{\Delta ABD}\ \cong\ \mathrm{\Delta BAC}\
(ii) BD = AC
(iii) \angle ABD\ =\ \angle BAC . 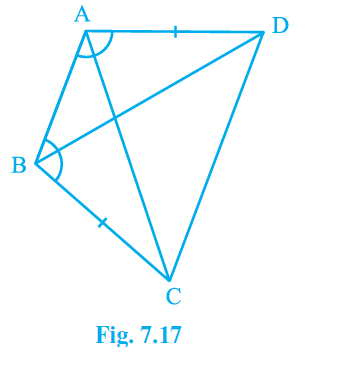
Answer: \angle DAB\ =\ \angle CBA and AD = BC are the supplied parameters from the questions.
\mathrm{\Delta ABD}\ and\ \mathrm{\Delta BAC} can be said similar by SAS congruency.
AB = BA (It is the common arm for both the triangles)
AD = BC and \angle DAB\ =\angle CBA (These are included in the question.)
Triangles \mathrm{\Delta ABD}\ and\ \mathrm{\Delta BAC}\ are hence similar, i.e. \mathrm{\Delta ABD}\ \cong\ \mathrm{\Delta BAC}\ (This is proved.)
Because it is now recognized that \mathrm{\Delta ABD}\ \cong\ \mathrm{\Delta BAC}\ ,
So, we can say BD=AC (according to the rule of C.P.C.T).
As because, \mathrm{\Delta ABD}\ \cong\ \mathrm{\Delta BAC}\
Therefore, we can write \angle ABD\ =\ \angle BAC (according to the rule of C.P.C.T).
Q3. AD and BC are equal perpendiculars to a line segment AB (see Fig. 7.18). Show that CD bisects AB. 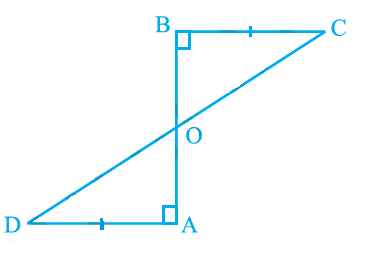
Answer:
AD and BC are two perpendiculars to AB that are equivalent.
We’ll have to show that CD is AB’s bisector.
AAS congruency links triangles \mathrm{\Delta AOD}\ and\ \mathrm{\Delta BOC} because:
\angle A=\angle B (because the angles are right angles)
AD=BC (mentioned in the question)
\angle AOD=\angle BOC (vertically opposite angles)
Therefore, we can write: \mathrm{\Delta AOD}\ \cong\ \mathrm{\Delta BOC} and AO=OB (according to the CPCT rule).
So, we can conclude that the line CD bisects the line AB.
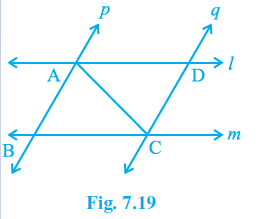
Q4. l and m are two parallel lines intersected by another pair of parallel lines p and q (see Fig. 7.19). Show that \mathrm{\Delta ABC}\ \cong\ \mathrm{\Delta CDA} .
Answer:
Provided data: p\ ||\ q\ \ and\ l\ ||\ m .
Considering the triangles ∆ABC and ∆ CDA .
\angle BCA=\angle DAC (alternate interior angles)
AC=CA (common arm for both the triangles)
\angle BAC=\angle DCA (alternate interior angles)
Therefore, using the ASA criteria of congruency we can write \mathrm{\Delta ABC}\ \cong\ \mathrm{\Delta CDA} .
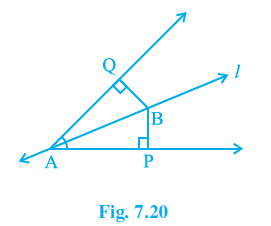
Q5. Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see Fig. 7.20). Show that:
(i) \mathrm{\Delta APB}\ \cong\ \mathrm{\Delta AQB}
(ii) BP = BQ or B is equidistant from the arms of ∠A.
Answer:
Provided data: The perpendiculars BP and BQ are derived from the line “l,” which is bisecting the angle A.
Considering triangles ∆APB and ∆AQB .
\angle P=\angle Q (right angles)
AB=BA (common arm for both the triangles)
\angle PAB=\angle QAB (line l is bisecting the angle A)
Therefore, using AAS rule of congruency we can write: \mathrm{\Delta APB}\ \cong\ \mathrm{\Delta AQB}
Using the rule of CPCT we can write: BP=BQ and B is at equal distance from arms of \angle A .
Q6. In Fig. 7.21, AC = AE, AB = AD and \angle BAD\ =\ \angle EAC . Show that BC = DE. 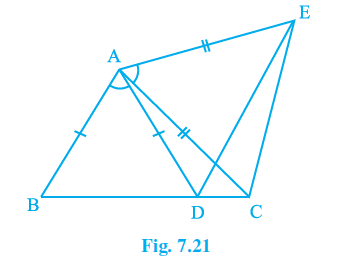
Answer:
Provided data: AC=AE,\ AB=AD\ \ and\ \angle BAD=\angle EAC .
Considering the triangles: ∆ABC and ∆ADE.
AC=AE (given)
AB=AD (given)
As it is given \angle BAD=\angle EAC , if we add angle \angle DAC to both the sides, we will get:
\angle DAC+\angle BAD=\angle EAC+\angle DAC
=> \angle BAC=\angle EAD
Using SAS rule of congruency, we can write: ∆ABC≅∆ADE
Also, we can write: BC=DE using CPCT rule.
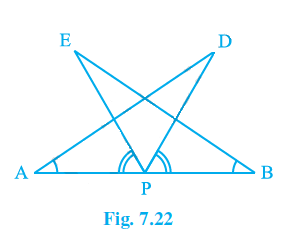
Q7. AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that \angle BAD\ =\ \angle ABE and \angle EPA\ =\ \angle DPB (see Fig. 7.22). Show that
(i) \mathrm{\Delta DAP}\ \cong\ \mathrm{\Delta EBP}
(ii) AD = BE
Answer:
P is the midpoint of line segment AB, as stated in the question. Furthermore, \angle BAD\ =\angle ABE and \angle EPA\ =\angle DPB .
Considering triangle \mathrm{\Delta DAP}\ and\ \mathrm{\Delta EBP}
AP = BP (Because P is the line segment AB’s midpoint)
\angle BAD\ =\ \angle ABE (Already mentioned in the question)
It is mentioned that \angle EPA\ =\angle DPB .
Add \angle DPE on both the sides of the above equation.
\angle DPB+\angle DPE\ =\angle EPA\ +\angle DPE
This means that DPA and EPB angles are equivalent, that is
\angle DPA\ =\ \angle EPB .
By using ASA rule of congruency, we can write \mathrm{\Delta DAP}\ \cong\ \mathrm{\Delta EBP} .
Now using CPCT rule we can write AD=BE.
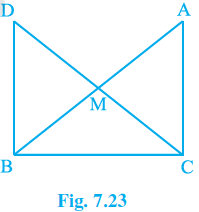
Q8. In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig. 7.23). Show that:
\angle DBC is a right angle.
\mathrm{\Delta DBC}\ \cong\ \mathrm{\Delta ACB}
CM\ =\frac{1}{2}\ AB
Answer:
Provided data: M is the mid-point of the line segment AB, \angle C\ =\ 90° , and DM = CM.
Consider the AMC and BMD triangles:
AM = BM (Because M is the middle point)
CM = DM (In response to the question)
\angle CMA\ =\ \angle DMB (vertically opposite angles)
As a result of the SAS congruency criteria, \mathrm{\Delta AMC}\ \cong\ \mathrm{\Delta BMD} .
By the rule of CPCT we can write: \angle ACM=\angle BDM
As because alternate interior angles are equivalent, AC || BD.
\angle ACB\ +\angle DBC\ =\ 180° (as because they are co-interiors angles)
We can write: {90}^o+\angle B={180}^o
Therefore, \angle DBC={90}^o
Considering triangles ∆ACB and ∆DBC
BC=CB (common arm for both the triangles)
\angle ACB\ =\ \angle DBC (right angles)
DP=AC (using CPCT rule)
So, according to SAS rule of congruency we can write: ∆ACB and ∆DBC .
Since ∆ACB and ∆DBC , DC = AB.
AM = BM = DM = CM (Because M is the midpoint)
As a result, DM + CM = BM+AM.
As a result, CM + CM = AB.
\Rightarrow\ CM\ =\ (½) AB
Exercise 7.2
Q1. In an isosceles triangle ABC, with AB = AC, the bisectors of \angle B\ and\ \angle C intersect each other at O. Join A to O. Show that:
OB = OC
AO bisects \angle A
Answer:
Provided data: AB Equals AC and
At O, the bisectors of \angle B and \angle C cross each other.
ABC is an isosceles triangle so that AB = AC.
\angle B\ =\ \angle C
\frac{1}{2}\angle B\ =\frac{1}{2}\angle C
\Rightarrow\ \angle OBC\ =\ \angle OCB\ (Angle bisectors)
∴ OB = OC (The side opposite the equal angles is the same.)
Considering triangles ∆AOB and ∆AOC
AB = AC (mentioned in the question)
AO = OA (Common arm for both the triangles)
OB = OC (Already proved in part (i) )
As a result, ∆AOB and ∆AOC by the SSS congruence requirement.
\angle BAO=\angle CAO (by the rule of CPCT)
As a result, AO bisects A.
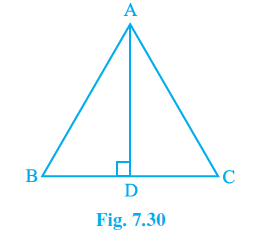
Q2. In ΔABC, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that ΔABC is an isosceles triangle in which AB = AC.
Answer:
Provided data: The perpendicular bisector of the arm BC is AD.
Considering triangles \mathrm{\Delta ADB}\ and\ \mathrm{\Delta ADC} .
AD = DA (Common arm for both the triangles)
\angle ADB\ =\ \angle ADC (right angles)
BD = CD (Because the perpendicular bisector is AD)
As a result, SAS congruency criteria \mathrm{\Delta ADB}\ and\ \mathrm{\Delta ADC} ..
Thus,
AB = AC (by the rule of CPCT).
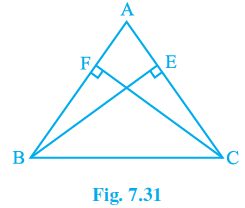
Q3. ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.
Answer:
Provided data: Altitudes are BE and CF.
AC = AB
Considering the triangles ∆AEB and ∆AFC .
\angle A\ =\ \angle A (common angle for both the triangles)
\angle AEB\ =\ \angle AFC (right angles)
AB = AC (Mentioned in the question)
AAS congruency makes triangles \mathrm{\Delta AEB}\cong\ \mathrm{\Delta AFC} .
So, we can write: BE=CF (using the rule of CPCT).
Q4. ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see Fig. 7.32). Show that
(i) \mathrm{\Delta ABE}\ \cong\ \mathrm{\Delta ACF}
(ii) AB = AC, i.e., ABC is an isosceles triangle.
Answer:
Provided data: BE=CF
Considering triangle \mathrm{\Delta ABE}\ and\ \mathrm{\Delta ACF}
\angle A\ =\ \angle A (common angle for both the triangles)
\angle AEB\ =\ \angle AFC (right angles)
BE = CF (mentioned in the question)
By the AAS congruency criterion, \mathrm{\Delta ABE}\ \cong\ \mathrm{\Delta ACF} .
We can write: AB=AC using the CPCT rule. Therefore, ABC can be said as an isosceles triangle.
Q5. ABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that \angle ABD\ =\ \angle ACD . 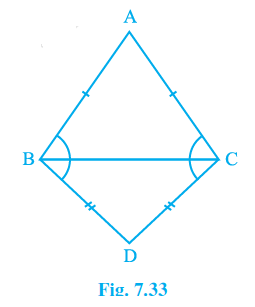
Answer:
ABC and DBC are the two isosceles triangles, as stated in the question.
Considering triangles \mathrm{\Delta ABD}\ and\ \mathrm{\Delta ACD} .
AD = AD (common arm for both the triangles)
AB = AC (An isosceles triangle is ABC.)
BD = CD (as because BCD is an isosceles triangle)
As a result, \angle ABD\ =\ \angle ACD .
By CPCT, \angle ABD\ =\angle ACD .
Q6. ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see Fig. 7.34). Show that ∠BCD is a 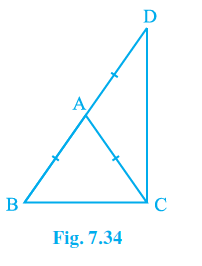
Answer:
AB = AC and AD = AB are mentioned in the question.
considering \mathrm{\Delta ABC} .
AB = AC (mentioned in the question)
Moreover, \angle ACB\ =\angle ABC (the angles that are opposite to equal sides are said to be equal)
Consider \mathrm{\Delta ACD} now.
AD = AB
Furthermore, \angle ADC\ =\angle ACD (the angles that are opposite to equal sides are said to be equal)
Now, \angle CAB\ +\ \angle ACB\ +\ \angle ABC Equals 180° in ∆ABC .
As a result, \angle CAB\ +\ 2\angle ACB\ =\ 180° and \angle CAB\ =\ 180° – 2∠ACB — (i)
\angle CAD\ Equals\ 180° – 2∠ACD in \ ∆ADC , and \angle CAB\ +\ \angle CAD\ =\ 180° in →CAB (as because BD is a straight line.)
\angle CAB\ +\ \angle CAD\ =\ 180° – 2∠ACB+180° – 2∠ACD
180° = 360° – 2∠ACB-2∠ACD
2(\angle ACB+\angle ACD)\ =\ 180°
\angle BCD={90}^o
Q7. ABC is a right-angled triangle in which \angle A\ =\ 90° and AB = AC. Find \angle B\ and\ \angle C . 
Answer:
It is stated in the question that:
AB\ =\ AC\ and\ \angle A\ =\ 90°
AB = AC
⇒ \ \angle B\ =\ \angle C (angles opposite to equal sides are equal)
\angle A+\angle B+\angle C\ =\ 180° (sum of the interior angle so a triangle is 180)
∴ 90° + 2∠B = 180°
⇒ \ 2\angle B\ =\ 90°
⇒ \angle B\ =\ 45°
So, \angle B\ =\ \angle C\ =\ 45°
Q8. Show that the angles of an equilateral triangle are 60° each.
Answer: Assume ABC is an equilateral triangle like this:
BC\ =\ AC\ =\ AB in this case. (Because both sides have the same length)
⇒ \angle A\ =\ \angle B\ =\angle C (Sides opposite to the equal angles are equal.)
We also know that
\angle A+\angle B+\angle C\ =\ 180°
⇒ 3\angle A\ =\ 180°
⇒ \angle A\ =\ 60°
∴ \angle A\ =\ \angle B\ =\ \angle C\ =\ 60°
An equilateral triangle's angles are always 60 degrees each.
Exercise 7.3
Q1. ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that
(i) \mathrm{\Delta ABD}\ \cong\ \mathrm{\Delta ACD}
(ii) \mathrm{\Delta ABP}\ \cong\ \mathrm{\Delta ACP}
(iii) AP bisects \angle A as well as \angle D .
(iv) AP is the perpendicular bisector of BC. 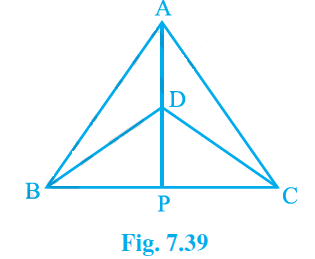
Answer:
∆ABC and DBC are two isosceles triangles, as stated in the question.
(i) SSS congruency compares ∆ABD and\ ∆ACD because:
AD = AD (It is the common arm)
AB = AC (Because ABC is an isosceles triangle)
(Because DBC is isosceles, BD = CD)
Therefore, we can write \mathrm{\Delta ABD}\ \cong\ \mathrm{\Delta ACD} .
(ii) ∆ABP and ∆ACP are similar in the following ways:
AP = AP (It is the common side)
\angle PAB\ =\ \angle PAC (by CPCT since ΔABD ≅ ΔACD)
AB = AC (Because ABC is an isosceles triangle)
So, \mathrm{\Delta ABP}\cong\mathrm{\Delta ACP} by SAS congruency condition.
(iii) By CPCT rule we can write: \angle PAB\ =\angle PAC because ∆ABD≅ ∆ACD .
Line AP cuts angle A in half (i)
∆BPD and ∆CPD are also similar in terms of SSS congruency.
PD = PD (It is the common side for both the triangles).
As Because ∆DBC is isosceles, we can write: BD = CD
BP = CP (abbreviated as ∆ABP≅∆ACP by CPCT)
Therefore, \ \mathrm{\Delta BPD}\ \cong\ \mathrm{\Delta CPD}
As a result, via CPCT, \angle BDP\ =\angle CDP-(ii) .
By comparing (i) and (ii), it may be concluded that AP bisects both angle A and angle D.
(iv) \ \angle BPD\ =\angle CPD (as defined by CPCT because ∆BPD≅∆CPD )
and BP = CP — (i)
also,
\angle BPD\ +\angle CPD\ =\ 180° (as because BC is a straight line.)
⇒ 2\angle BPD\ =\ 180°
⇒ \angle BPD\ =\ 90° — (ii)
Now, we may deduce from equations (i) and (ii) that
The perpendicular bisector of BC is AP.
Q2. AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC (ii) AD bisects ∠A.
Answer: AD is an altitude, and AB = AC. The illustration is as follows: 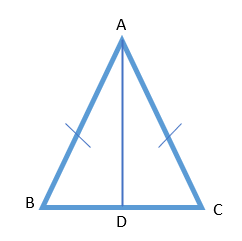
Considering the triangles ∆ABD and ∆ACD .
We can write: \angle ADB=\angle ADC={90}^o because AD is an altitude.
AB=AC (mentioned in the question)
AD=DA (common arm for both the triangles)
Therefore, we can write ∆ABD≅ACD by the condition of RHS.
Now, with the rule of CPCT we can write: BD=CD
Therefore, we can say that AD bisects BC.
By using the rule of CPCT we can write that \angle BAD=\angle CAD
Therefore, AD bisects the angle A.
Q3. Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see Fig. 7.40). Show that:
(i) \mathrm{\Delta ABM}\ \cong\ \mathrm{\Delta PQN}
(ii) \mathrm{\Delta ABC}\ \cong\ \mathrm{\Delta PQR} 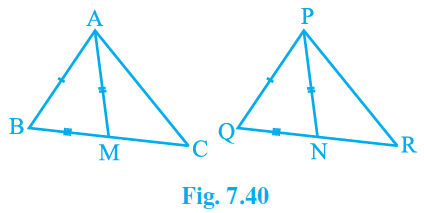
Answer:
The given parameters we have:
AB=PQ,
BC=QR,
AM=PN
We can write: \frac{1}{2}BC=BM\ \ and\frac{1}{2}QR=QN because the AM and PN are the medians.
Moreover, BC = QR
therefore, ½ BC = ½ QR
⇒ BM = QN
In ∆PQN and ∆ABM ,
AB = PQ, AM = PN (As stated in the question)
BM = QN (we have Already proved)
By SSS congruency, we can write ∆ABM≅∆PQN .
In the ∆ABC and ∆PQR ,
BC = QR and AB = PQ (As stated in the question)
\angle ABC\ =\ \angle PQR (by the rule of CPCT)
As a result, according to SAS criteria of congruency we can write: ∆ABC≅∆PQR .
Q4. BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
Answer:
BE and CF are known to be two equal elevations.
Currently, in ∆BEC and ∆CFB ,
\angle BEC\ =\ \angle CFB\ =\ 90° (they have the same Altitudes)
BC = CB (Common side for both the triangles)
BE = CF (Common side for both the triangles)
By the RHS congruence criteria, \mathrm{\Delta BEC}\ \cong\ \mathrm{\Delta CFB}
Also, \angle C\ =\ \angle B (by the rule of CPCT)
As the sides opposing the equal angles are always equal, AB = AC.
Q5. ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that \angle B\ =\ \angle C
Answer:
It is stated that AB Equals AC in the question.
By RHS congruency, we can write ∆ABP≅∆ACP because:
\angle APB\ =\ \angle APC\ =\ 90° (AP is altitude)
AB = AC (mentioned in the question)
AP = AP (Common side for both the triangles)
As a result, ∆ABP≅∆ACP .
∴ \angle B\ =\ \angle C (by th4e rule of CPCT).
Exercise 7.4
Q1. Show that in a right-angled triangle, the hypotenuse is the longest side.
Answer:
ABC is known to be a right-angled triangle at B.
We're aware that:
\angle A\ +\angle B+\angle C\ =\ 180°
If angle A+ angle C Equals 90°, then B must also be 90°.
Because B is the triangle's biggest angle, the side opposite it must also be the largest.
As a result, AC is the hypotenuse, which is the greatest side of the right-angled triangle ABC.
Q2. In Fig. 7.48, sides AB and AC of ΔABC are extended to points P and Q respectively. Also, \angle PBC\ <\ \angle QCB . Show that AC > AB. 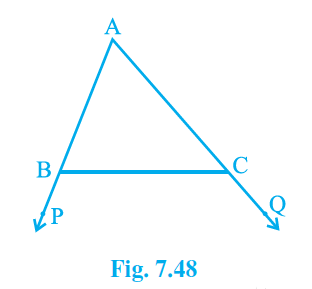
Answer:
It is mentioned that \angle PBC<\angle QCB.
We already know that \angle ABC\ +\angle PBC Equals 180 degrees.
As a result, \angle ABC\ =\ 180°-∠PBC .
Also,
\angle ACB\ +\angle QCB\ =\ 180°
As a result, \angle ACB\ =\ 180° -∠QCB .
As because \angle PBC<\angle QCB.
∴ \angle ABC\ >\ \angle ACB
As a result, AC > AB because the sides opposing the bigger angle are always larger.
Q3. In Fig. 7.49, \angle B\ <\ \angle A and \angle C\ <\ \angle D . Show that AD < BC. 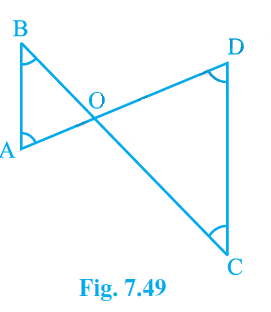
Answer:
Angles B and C are smaller than angles A and D, respectively, as stated in the question, that is \angle B<\angle A\ and\ \angle C<\angle D .
Now,
Because the smaller angle's opposite side is always smaller,
AO < BO — (i)
And OD < OC — (ii)
By multiplying equations, (i) and (ii), we obtain
AO+OD<BO+OC
Therefore, we can write: AD</p><p>Q4. AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see Fig. 7.50).
Show that \angle A\ >\ \angle C and \angle B\ >\ \angle D . 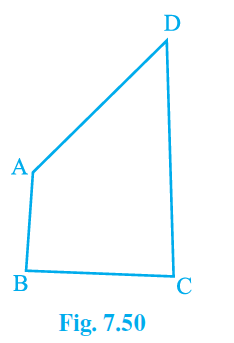
Answer:
We can see in ABD that
AB\ <\ AD\ <\ BD
As a result, \angle ADB<\angle ABD — (i) (As because the angle opposite to longer side is always larger)
Currently, in ∆BCD ,
BC\ <\ DC\ <\ BD
As a result, it may be stated that
\angle BDC\ <\ \angle CBD — (ii)
By multiplying equations (i) and (ii), we get:
\angle ADB\ +\angle BDC<\angle ABD\ +\angle CBD
\angle ADC\ <\ \angle ABC
\angle B\ >\ \angle D
Similarly, in the ABC triangle,
\angle ACB<\angle BAC — (iii) (As because the angle opposite to the longer side is always larger)
Currently, in ∆ADC ,
\angle DCA\ <\ \angle DAC — (iv)
By multiplying equations (iii) and (iv), we get
\angle BAC\ +\angle DCA<\angle BAC\ +\angle DAC
⇒ \angle BCD\ <\ \angle BAD
Therefore, \angle A\ >\ \angle C .
Q5. In Fig 7.51, PR > PQ and PS bisect \angle QPR . Prove that \angle PSR\ >\ \angle PSQ . 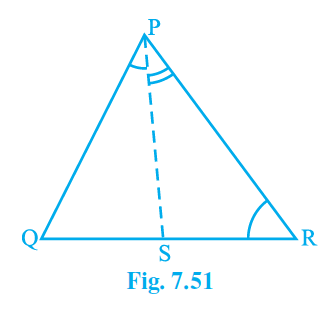
Answer:
It is already mentioned in the question that: PR > PQ, and PS bisects \angle QPR .
\angle PQR\ >\angle PRQ — (i) (Because the angle opposing the larger side is always larger, PR > PQ)
Since PS bisects \angle QPR we can write \angle QPS\ =\angle RPS -(ii)
\angle PSR\ =\angle PQR\ +\angle QPS — (iii) (as because the sum of the exerior angle of a triangle is equal to sum of opposite interior angles)
\angle PSQ\ =\angle PRQ\ +\angle RPS -(iv) (as because the sum of the exterior angle of a triangle is equal to sum of opposite interior angles)
By combining (i) with (ii) we can write
\angle PQR\ +\angle QPS>\angle PRQ\ +\angle RPS
As a result of (i), (ii), (iii), and (iv), we have
\angle PSR\ >\ \angle PSQ .
Q6. Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest. 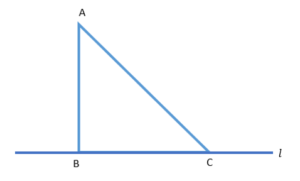
Answer:
Let "l" represent a line segment and "B" represent a point lying on it. Now draw a line AB perpendicular to l. Let C be any other point on l as well. The diagram will look like this:
In \mathrm{\Delta ABC},\ \angle B\ =\ 90°
We now know that
\angle A+\angle B+\angle C\ =\ 180°
∴ \angle A\ +\angle C\ =\ 90°
As a result, \angle C must be an acute angle, implying \angle C<\angle B.
Therefore, AB\ <\ AC (Due to the fact that the side opposite the bigger angle is always larger)
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out