NCERT Solutions Class 9 Maths Chapter 6-Lines And Angles

Exercise 6.1

Q1. In Fig. 6.13, lines AB and CD intersect at O. If 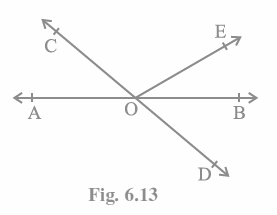\angle AOC\ +\angle BOE\ =\ 70° and \angle BOD\ =\ 40°, find ∠BOE and reflex ∠COE.

Answer:

We can see from the diagram that
A straight line is formed by (\angle AOC\ +\angle BOE\ +\angle COE) and (\angle COE\ +\angle BOD\ +\angle BOE).
As a result, \angle AOC+\angle BOE\ +\ \angle COE =\ \angle COE\ +\angle BOD+\angle BOE\ =\ 180°
Putting the values of \angle AOC\ +\ \angle BOE\ =\ 70° and \angle BOD\ =\ 40° together yields
\angle BOE\ =\ 30° and ∠COE = 110°
Thus, \angle COE\ =\ {360}^o\ –\ {110}^o\ = \ {250}^o\ .

Q2. In Fig. 6.14, lines XY and MN intersect at O. If ∠POY = 90° and a : b = 2 : 3, find c.

Answer:

We already know that the total of linear pairs is always 180°. 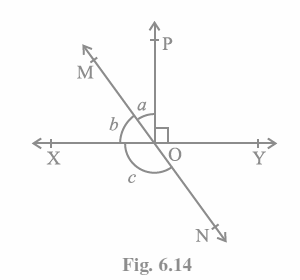So,
\angle POY\ +a\ +b\ =\ 180°
We obtain, when we put the value of \angle POY\ =\ 90° (as specified in the question),
a+b\ =\ 90°
Now, because a: b = 2: 3 is known,
Let an equal 2x and b equal 3x.
Therefore, 2x+3x\ =\ 90°
When we solve this, we obtain
5x\ =\ 90°
So,\ x\ =\ 18°
\therefore\ a\ =\ 2\times18° = 36°
In similar way, b can be computed, with the result being
b = 3×18° = 54°
B+c also creates a straight angle in the diagram, thus
b+c = 180°
c+54° = 180°
∴ c = 126°

Q3. In Fig. 6.15, \angle PQR\ =\ \angle PRQ, then prove that 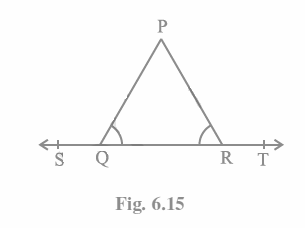\angle PQS\ =\ \angle PRT.

Answer:

Given that ST is a straight line,
\angle PQS+\angle PQR\ =\ 180° degrees (linear pair)
\angle PRT+\angle PRQ\ =\ 180° (linear pair)
\angle PQS\ +\ \angle PQR\ =\ \angle PRT+\angle PRQ\ =\ 180° now
Because \angle PQR\ =\ \angle PRQ (as mentioned in the question)
\angle PQS\ =\ \angle PRT (Hence proved).

Q4. In Fig. 6.16, if x + y = w + z, then prove that AOB is a line. 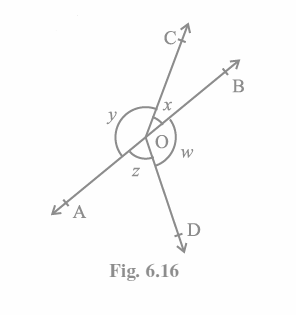Answer:

To show that AOB is a straight line, we must first show that x+y is a linear pair.
i.e. x+y\ =\ 180°
We know that there are 360 degrees of angles surrounding a point, so
x+y+w+z\ =\ 360°
It is stated in the question that,
x + y Equals w + z
So, (x+y)+(x+y)\ =\ 360°
2(x+y)\ =\ 360°
∴ (x+y)\ =\ 180° (Proved).

Q5. In Fig. 6.17, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that \angle ROS\ =\frac{1}{2}\ (∠QOS – ∠POS). 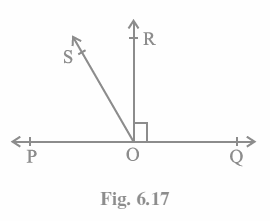Answer:

It is stated in the question that \left(OR\bot P Q\right)and\ \angle POQ\ =\ 180°
Therefore, \angle POS\ +\ \angle ROS\ =\ 90°
Now, \angle QOS\ = \angle ROQ+\angle ROS.
Given that \angle ROQ\ =\ 90 degrees,
∴ \angle QOS\ =\ 90° +∠ROS
Alternatively, \angle QOS\ – ∠ROS = 90°
We get \angle POS\ +\ \angle ROS\ =\ 90° and ∠QOS – ∠ROS = 90°.
\angle QOS\ – ∠ROS = ∠POS + ∠ROS.
2\ \angle QOS\ =\ \angle ROS\ +\ \angle POS
Alternatively, ROS\ =\frac{1}{2}\ (\angle QOS\ – ∠POS) (Proved)..

Q6. It is given that ∠XYZ = 64° and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ZYP, find ∠XYQ and reflex ∠QYP. 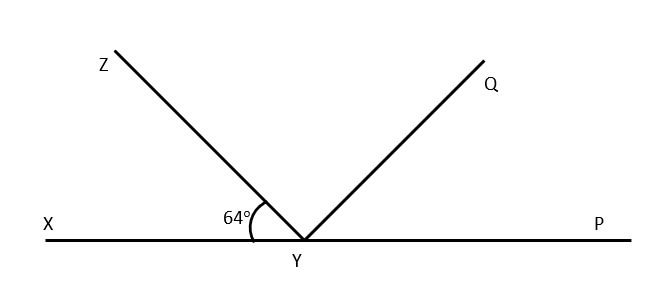Answer:

In the diagram we can observe XP is a straight line
Thus, \angle XYZ\ +\ \angle ZYP\ =\ 180°.
We get, by substituting the value of \angle XYZ\ =\ 64°,
64° +∠ZYP = 180°
∴ \angle ZYP\ =\ 116°
We also know that \angle ZYP\ =\ \angle ZYQ\ +\ \angle QYP from the diagram.
Now that YQ has bisected \angle ZYP,
\angle ZYQ\ =\ \angle QYP
Alternatively, \angle ZYP\ =\ 2\angle ZYQ
∴ \angle ZYQ\ =\ \angle QYP\ =\ 58°
\angle XYQ\ =\ \angle XYZ\ +\ \angle ZYQ once again.
We get by combining the values of \angle XYZ\ =\ 64° and ∠ZYQ = 58°.
\angle XYQ\ =\ 64°+58°
=> \angle XYQ\ =\ 122°
Now, \angle QYP\ =\ 180°+∠XYQ is the reflex.
The value of \angle XYQ\ =\ 122° was calculated.
therefore,
\angle QYP\ =\ 180°+122°
\angle QYP\ =\ 302°

Exercise 6.2

Q1. In Fig. 6.28, find the values of x and y and then show that AB || CD. 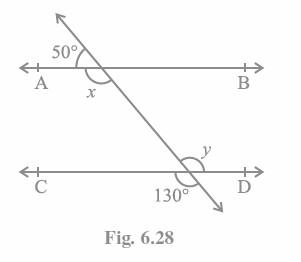Answer:

A linear pair equals 180 degrees, as we know.
So, we can write, x+50° = 180°
∴ x = 130°
Vertically opposite angles are also equal.
Thus, y = 130°
The alternate interior angles of two parallel lines are equivalent. here,
x = y = 130°
As a result, AB || CD establishes that alternate interior angles are equivalent.

Q2. In Fig. 6.29, if AB || CD, CD || EF and y : z = 3 : 7, find x. 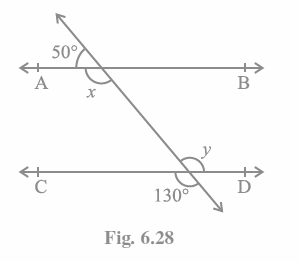Answer:

It is mentioned in the question that AB || CD and CD||EF
Because the sum of the angles on the same side of a transversal line is 180°,
x + y = 180° – (i)
Also,
\angle O\ =\ z They’re corresponding angles, thus
we can write, y\ +\angle O\ =\ 180° because they are linear pairs
Hence, y+z = 180°
Let us assume y = 3w and hence z = 7w (since y: z = 3: 7)
∴ 3w+7w\ =\ 180°
Alternatively, 10\ w\ =\ 180°
Therefore, w = 18°
Now, y\ =\ 3\times18° = 54°
therefore, z\ =\ 7\times18° = 126°
Angle x can now be computed using equation (i)
x+y\ =\ 180°
Or,\ x+54° = 180°
\therefore\ x\ =\ 126°

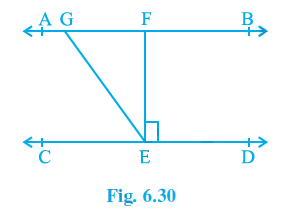
Q3. In Fig. 6.30, if AB || CD, EF ⊥ CD and \angle GED\ =\ 126°, find ∠AGE, ∠GEF and ∠FGE.

Answer:

GE can be called as transversal since AB || CD.
\angle GED\ =\ 126° is mentioned
As a result, \angle GED\ =\angle AGE\ =\ 126°. (Alternate interior angles)
Also,
\angle GED\ =\angle FED\ +\angle GEF
\angle FED\ =\ 90° as EFCD
∴ \angle GED\ =\ \angle GEF+90°
Alternatively, \angle GEF\ =\ 126° – 90° = 36°
\angle FGE\ +\angle GED\ =\ 180° once again (Transversal)
We get, when we put the value of \angle GED\ =\ 126°,
\angle FGE\ =\ 54°
So,
\angle AGE\ =\ 126°
\angle GEF\ =\ 36°
\angle FGE\ =\ 54°

Q4. In Fig. 6.31, if PQ || ST, ∠PQR = 110° and ∠RST = 130°, find ∠QRS.
[Hint: Draw a line parallel to ST through point 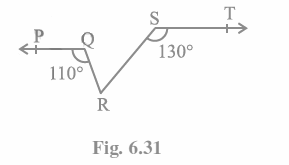R.] Answer:

The angles situated on the same side of a transversal are equivalent to 180° degrees.
As a result, \angle PQR+\angle QRX\ =\ 180°.
Alternatively, \angle QRX\ =\ 180°-110°
∴ \angle QRX\ =\ 70°
Likewise,
\angle RST\ +\angle SRY\ =\ 180°
Alternatively, \angle SRY\ =\ 180°- 130°
∴ \angle SRY\ =\ 50°
Now we will be considering the linear pairs on the XY-axis.
180° =∠QRX+∠QRS+∠SRY
When we add their values together, we get
\angle QRS\ =\ 180° – 70° – 50°
As a result, \angle QRS\ =\ 60°.

Q5. In Fig. 6.32, if AB || CD, ∠APQ = 50° and ∠PRD = 127°, find x and y. 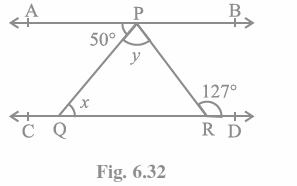Answer:

According to the diagram,
\angle APQ\ =\ \angle PQR (Alternate interior angles)
Putting the values of \angle APQ\ =\ 50°\ and\ ∠PQR = x together, we get:
x = 50°
Also,
\angle APR\ =\ \angle PRD (Alternate interior angles)
Alternatively, \angle APR\ =\ 127° (as because \angle PRD\ =\ 127°)
We’re aware of this.
\angle APR equals \angle APQ+\angle QPR.
substituting the values of \angle QPR\ =\ y\ and\ \angle APR\ =\ 127° together, we get:
127° = 50°+ y
Or,\ y\ =\ 77°
As a result, the x and y values are calculated as:
x = 50° and y = 77°

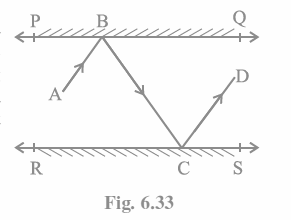
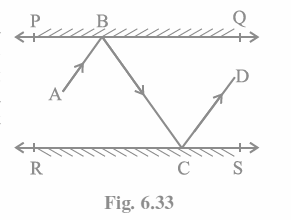
Q6. In Fig. 6.33, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB || CD. Answer:

To begin with, draw two lines BE and CF that intersect at BE PQ and CF RS.
As because PQ || RS,
Thus, BE || CF
We’re aware of this.
Angle of reflection = Angle of incidence (According to the law of reflection)
So,
a = b and
c = d
We also know that interior angles on both sides are equal. BE CF and the transversal line BC cut them at B and C in this case.
So, b = c (As they are alternate interior angles)
Now, a +b = c +d
Alternatively, ABC = DCB
So, AB || CD (as because alternate interior angles are equal)

Exercise 6.3

Q1. In Fig. 6.39, sides QP and RQ of ΔPQR are produced to points S and T respectively. If ∠SPR = 135° and ∠PQT = 110°, find ∠PRQ. 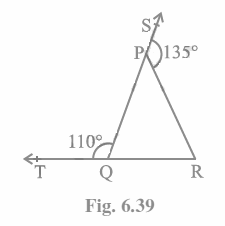Answer:

Because the TQR is a straight line, the linear pairs (\angle TQP\ and\ \angle PQR) will add up to 180°
Thus, \angle TQP\ +\ \angle PQR\ =\ 180°.
Now, if we take the value of \angle TQP\ =\ 110° degrees, we get:
\angle PQR\ =\ 70°
Think about the PQR.
The side QP is extended to S in this case, forming the external angle SPR.
As a result, the total of internal opposite angles equals \angle SPR\ (\angle SPR\ =\ 135°). (Property triangle)
Alternatively, \angle PQR\ +\ \angle PRQ\ =\ 135°
Putting the value of \angle PQR\ =\ 70° together, we get
\angle PRQ\ =\ 135°-70°
As a result, \angle PRQ\ =\ 65°.

Q2. In Fig. 6.40, ∠X = 62°, ∠XYZ = 54°. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of Δ XYZ, find ∠OZY and ∠YOZ. 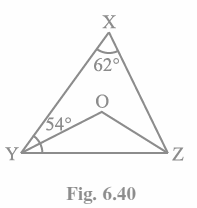Answer:

The sum of the internal angles of the triangle is known.
Therefore, \angle X\ +\angle XYZ\ +\angle XZY\ =\ 180°.
Using the values in the question as a guide,
62°+54° +∠XZY = 180°
Alternatively, \angle XZY\ =\ 64°
Now that we know ZO is the bisector,
\angle OZY\ =\frac{1}{2}\ ∠XZY
\therefore\ \angle OZY\ =\ 32°
Likewise, YO is a bisector, thus
\angle OYZ\ =\frac{1}{2}\ ∠XYZ
Alternatively, \angle OYZ\ =\ 27° (as because ∠XYZ = 54°)
Now, the total of the triangle’s interior angles is
\angle OZY\ +\angle OYZ\ +\angle O\ =\ 180°
When we add their values together, we get
\angle O\ =\ 180°-32°-27°
Thus, \angle O\ =\ 121°

Q3. In Fig. 6.41, if AB || DE, ∠BAC = 35° and ∠CDE = 53°, find ∠DCE. 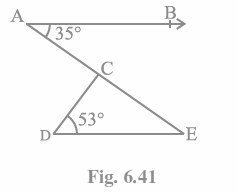Answer:

Since AB || DE, we can say that AE is a transversal.
The internal angles \angle BAC\ and\ \angle AED are alternate here.
As a result, \angle BAC\ =\angle AED
It is assumed that \angle BAC\ =\ 35 degrees.
∠AED = 35°
Considering the CDE triangle. We know that the sum of a triangle’s internal angles is 180 degrees.
\angle DCE+\angle CED+\angle CDE\ =\ {180}^o
When we combine the values, we get
\angle DCE+35°+53° = 180°
As a result, \angle DCE\ =\ 92°

Q4. In Fig. 6.42, if lines PQ and RS intersect at point T, such that ∠PRT = 40°, ∠RPT = 95° and ∠TSQ = 75°, find ∠SQT. 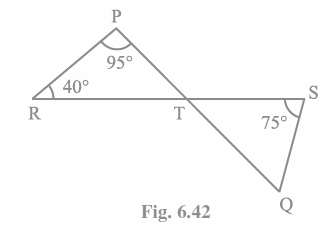Answer:

Consider the PRT triangle.
180° =∠PRT +∠RPT +∠PTR
So, ∠PTR = 45°
Due to their vertically opposite angles, PTR and STQ will now be equal.
As a result, \angle PTR\ =\angle STQ\ =\ 45°.
In triangle STQ once more,
180° =∠TSQ +∠PTR +∠SQT
We arrive to a solution.
74° + 45° + ∠SQT = 180°
∠SQT = 60°

Q5. In Fig. 6.43, if PQ ⊥ PS, PQ || SR, ∠SQR = 28° and ∠QRT = 65°, then find the values of x and y. 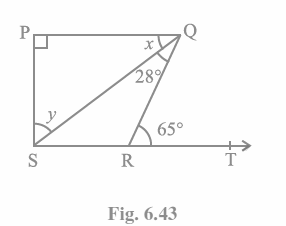Answer:

We can write \angle x\ +\angle SQR\ =\ \angle QRT (As because they are alternate angles since QR is transversal)
So, x+28° = 65°
Therefore x = 37°
Alternate interior angles are also known to be the same, so
\angle QSR\ =\ x\ =\ 37°
Also, Now,
\angle QRS\ +\angle QRT\ =\ 180° (Linear pair)
Alternatively, \angle QRS+65° = 180°
Thus, \angle QRS\ =\ 115°
In ∆SPQ, the angle sum attribute is used.
\angle SPQ\ +\ x\ +\ y\ =\ 180°
When we add their values together, we get
90°+37° + y = 180°
y\ =\ 1800\ – 1270 = 530
Therefore, y = 53°

Q6. In Fig. 6.44, the side QR of ΔPQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR = \frac{1}{2}\ ∠QPR. 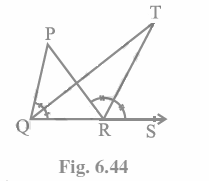Answer:

Considering about the triangle PQR. The external angle is PRS, and the inside angles are QPR and PQR.
As a result, \angle PRS\ =\angle QPR+\angle PQR (According to triangle property)
Alternatively, \angle PRS\ -\angle PQR\ =\angle QPR– (i)
Consider the ∆QRT now.
\angle TRS\ =\angle TQR+\angle QTR
Alternatively, \angle QTR\ =\angle TRS-\angle TQR
\angle PQR\ and\ \angle PRS are bisected by QT and RT, respectively.
As a result, \angle PRS\ =\ 2\ \angle TRS and \angle PQR\ =\ 2\ \angle TQR.
\angle QTR\ =\frac{1}{2}\ \angle PRS\ -\frac{1}{2}∠PQR now.
Alternatively, \angle QTR\ =\frac{1}{2}\ (\angle PRS\ -\angle PQR)
We know that \angle PRS\ -\angle PQR\ =\angle QPR from (i)
As a result, \angle QTR\ =\frac{1}{2}\ \angle QPR (hence proved).