NCERT Solutions for Class 9 Maths Chapter 11 Constructions are provided here for the convenience of Class 9 students. Geometry is a fundamental concept that can be applied in a variety of fields. As a result, it is essential to learn the concept and comprehend its applications. The NCERT Solutions for Class 9 Maths Chapter 11 Constructions are the best way to learn this concept. These solutions are created by teachers who can effectively articulate concepts in order to help students ace their second term CBSE Class 9 Maths examination.
As a result, NCERT Solutions is the study guide you should use because the content is presented in a comprehensive format. We make certain that the instructions are simple and straightforward. Furthermore, we make certain that our content is up to date with the most recent CBSE Syllabus and guidelines.
NCERT Solutions for Class 9 Maths - Constructions PDF preview
Exercise 11.1
Question 1.
Construct an angle of 90° at the initial point of a given ray and justify the construction.
Construction Procedure:
Follow these steps to make a 90-degree angle:
Make an OA ray
Draw an arc DCB that cuts OA at B, using O as the center with any radius.
Draw a point C on the arc DCB with B as the center and the same radius.
Draw a point D on the arc DCB with C as the center and the same radius as C.
Starting at C and D, draw two arcs that cross at P and have the same radius.
Finally, the ray OP is linked, resulting in a 90° angle with OP. 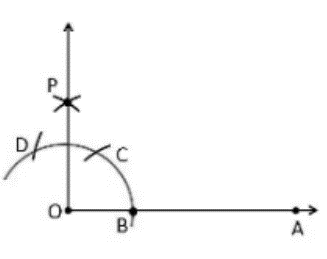
Justification
To prove
\angle POA\ =\ 90°
In order to prove this, draw a dotted line from the point O to C and O to D and the angles formed are: 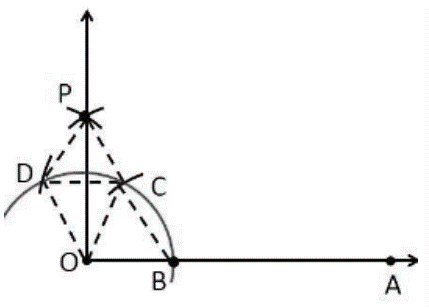
From the construction, it is observed that
OB\ =\ BC\ =\ OC
Therefore, OBC is an equilateral triangle
So that,
\angle BOC\ =\ 60°.
Similarly,
OD\ =\ DC\ =\ OC
Therefore, DOC is an equilateral triangle
So that,
\angle DOC\ =\ 60°.
Now, From SSS triangle congruence rule
\triangle OBC\ \cong\ OCD
So,
\angle BOC\ =\ \angle DOC [By C.P.C.T]
Therefore,
\angle COP\ =\frac{1}{2}\ \angle DOC\ =\frac{1}{2}\ (60°).
\angle COP\ =\ 30°
To find the
\angle POA\ =\ 90°:
\angle POA\ =\ \angle BOC+\angle COP
\angle POA\ =\ 60°+30°
\angle POA\ =\ 90°
Hence, justified.
Question 2.
Construct an angle of 45° at the initial point of a given ray and justify the construction.
Construction Procedure:
Make an OA ray
Draw an arc DCB that cuts OA at B, using O as the center with any radius.
Draw a point C on the arc DCB with B as the center and the same radius.
Draw a point D on the arc DCB with C as the center and the same radius as C.
Starting at C and D, draw two arcs that cross at P and have the same radius.
Finally, the ray OP is linked, resulting in a 90° angle with OP.
Using B and Q as a starting point, construct a perpendicular bisector that intersects at R.
Draw a line connecting points O and R.
As a result, the angle created was \angle ROA\ =\ 45°.
Justification
From the above construction,
\angle POA\ =\ 90°
From the perpendicular bisector from the point B and Q, which divides the ∠POA into two halves. So it becomes
\angle ROA\ =\frac{1}{2}\angle POA
\angle ROA\ =\ \left(\frac{1}{2}\right)\times90° = 45°
Hence, justified
Question 3.
Construct the angles of the following measurements:
30°
22{\frac{1}{2}}^0
15°
Solution:
30^0
Construct Procedure:
Draw an OA ray
Draw an arc BC that cuts OA at B, using O as the center with any radius.
Draw two arcs that overlap at point E, and the perpendicular bisector is created, using B and C as centers.
As a result, EOA is the required angle to make 30 degrees with OA. 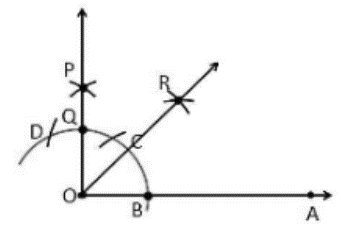
22{\frac{1}{2}}^0
Construction Procedure:
Draw a 90-degree angle (\angle POA).
Draw an arc BC that cuts\ OA at\ B and OP at Q, using\ O as the center with any radius.
Now draw the bisector between points B and Q, intersecting at point R, and making an angle of \angle ROA\ =\ 45°.
∠ROA is bisected once more, resulting in ∠TOA, which forms a 22.5° angle with OA. 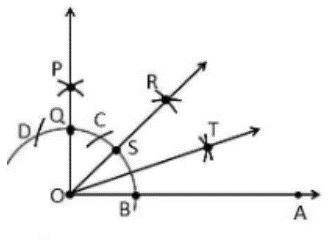
{15}^0
Construction Procedure:
A 60° DOA angle is drawn.
Draw an arc BC that cuts OA\ at B and OD at C, with\ O as the center and any radius.
Now draw the bisector between points B and C, intersecting at point E, and making an angle of [Katex] \angle EOA\ =\ 30°.[/katex]
\angle EOA is bisected once more, resulting in \angle FOA, which forms a 15° angle with OA.
As a result, \angle FOA is the needed angle, which is 15° with OA. 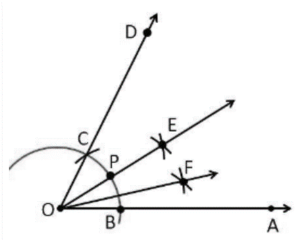
Question 4.
Construct the following angles and verify by measuring them by a protractor:
75° (ii) 105° (iii) 135°
Solution:
75^0
Construction Procedure:
The OA ray is drawn.
Draw an arc of any radius with O as the centre and intersect it at point B on the ray OA.
Draw an arc C with B as the centre and an arc D with\ C\ as the centre.
Draw an arc with D and C as the centres, intersecting at P.
Connect the\ O and\ P points.
Q\ is the location where the arc intersects the ray OP.
Draw an arc with Q\ and C\ as the centre points, intersecting at R.
Connect the O and R\ points.
As a result, \angle AOE is the needed angle when OA is 75 degrees. 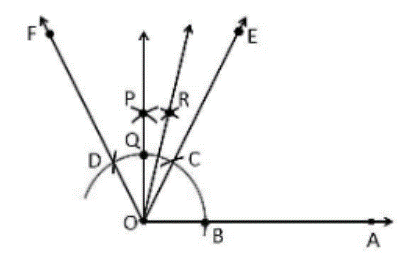
105^0
Construction Procedure:
An OA ray is created.
Draw an arc of any radius with O as the centre and intersect it at point B on the ray OA.
Draw an arc C with B as the centre and an arc D with C as the centre.
Draw an arc with D and C as the centres, intersecting at P.
Connect the O and P points.
Q is the location where the arc intersects the ray OP.
Draw an arc with Q and D as the centre points, intersecting at R.
Connect the O and R points.
As a result, ∠AOR is the needed angle, which is 105° with OA. 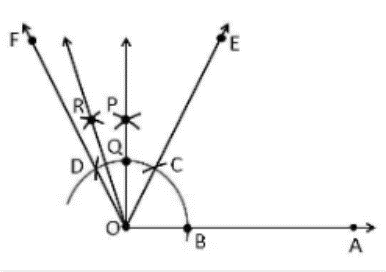
{135}^0
Construction Procedure:
Draw an AOA\prime line.
Draw an arc of any radius that intersects the line AOA\primeat B and B’.
Draw an arc of the same radius at point C with B as the center.
At point D, draw an arc with the same radius as C.
Draw an arc between D and C that intersects at point P.
Join OP
Q is the place where the arc intersects the ray OP, forming a 90° angle.
Draw an arc that connects at the point R with B’ and Q as the center.
As a result, \angle AOR is the needed angle, which is 135° with OA. 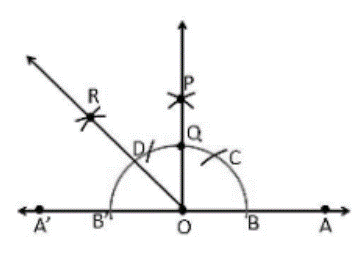
Question 5.
Construct an equilateral triangle, given its side and justify the construction.
Construction Procedure:
Let’s draw a line segment with the length AB = 4 cm.
Draw two arcs on the line segment AB with A and B as the centres, and label the points D and E.
Draw the arcs that cut the previous arc and make a 60° angle each with D and E as the centres.
Connect the lines A and B at C.
As a result, ABC is the necessary triangle. 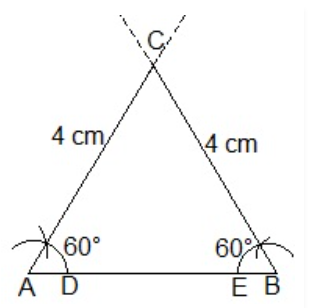
Justification
From construction, it is observed that
AB\ =\ 4\ cm,\ \angle A\ =\ 60° and ∠B = 60°
We know that, the sum of the interior angles of a triangle is equal to 180°
\angle A+\angle B+\angle C\ =\ 180°
Substitute the values
</p><p>\Rightarrow\ 60°+60°+∠C = 180°
\Rightarrow\ 120°+∠C = 180°
\Rightarrow\angle C\ =\ 60°
After measuring the sides, we get
BC\ =\ CA\ =\ 4\ cm (Sides opposite to equal angles are equal)
AB\ =\ BC\ =\ CA\ =\ 4\ cm
\angle A\ =\ \angle B\ =\ \angle C\ =\ 60°
Hence, justified.
Exercise 11.2
Question 1.
Construct a triangle ABC in which BC = 7cm, ∠B = 75° and AB+AC = 13 cm.
Construction Procedure:
To draw the triangle of a given measurement, follow these steps:
Draw a base BC\ =\ 7 cm line segment.
Draw the ray BX and measure and draw \angle B\ =\ 75°.
Using a compass, determine that AB+AC = 13 cm.
Draw an arc at the point D with B as the center.
Join DC
Draw the perpendicular bisector of the line DC, with A as the junction point.
Finally, join AC.
As a result, ABC is the necessary triangle. 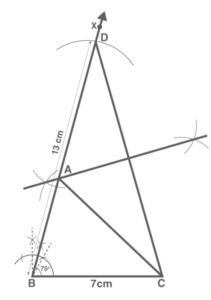
Question 2.
Construct a triangle ABC in which BC = 8cm, ∠B = 45° and AB–AC = 3.5 cm.
Construction Procedure:
To draw the triangle of a given measurement, follow these steps:
Draw a base BC\ =\ 8\ cm line segment.
Draw the ray BX and measure and draw ∠B = 45°.
Using a compass, find\ AB-AC\ =\ 3.5\ cm.
Draw an arc at the point D on the ray BX with B as the centre.
Join DC
Draw the perpendicular bisector of the line\ CD, with A as the intersection point.
Finally, join AC.
As a result, ABC is the necessary triangle. 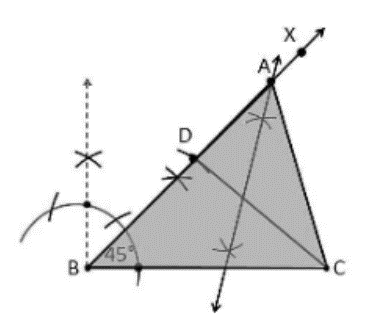
Question 3.
Construct a triangle PQR in which QR = 6cm, \angleQ = 60° and PR–PQ = 2cm.
Construction Procedure:
To draw the triangle of a given measurement, follow these steps:
Draw a 6 cm base QR line segment.
Measure and draw ∠Q = 60°, with QX as the ray.
Using a compass, find PR–PQ = 2cm.
QD will be below the line QR since PR–PQ is negative.
Draw an arc at the point D on the ray QX with Q as the centre.
Join DR
Now draw the line DR’s perpendicular bisector, with P as the junction point.
Finally, join PR.
As a result, PQR is the necessary triangle. 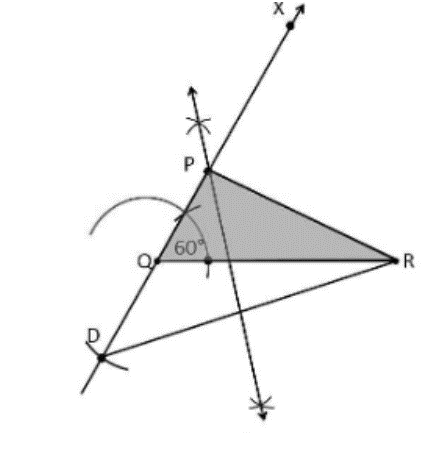
Question 4.
Construct a triangle XYZ in which \angle Y\ =\ 30°, \angle Z\ =\ 90° and XY+YZ+ZX\ =\ 11\ cm.
Construction Procedure:
To draw the triangle of a given measurement, follow these steps:
Draw an AB line segment with the length XY+YZ+ZX\ =\ 11\ cm.
From point A, make an angle of \angle LAB\ =\ 30°.
From point B, make an angle of \angle MBA\ =\ 90°.
At point X, divide \angle LAB\ and\ \angle MBA.
Let the perpendicular bisector of the lines XA and XB be\ Y and Z, respectively, and the intersection point be\ Z.
Bring\ XY and XZ together.
As a result, the needed triangle is XYZ. 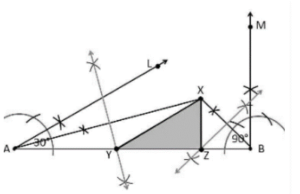
Question 5.
Construct a right triangle whose base is 12cm and sum of its hypotenuse and other side is 18 cm.
Construction Procedure:
To draw the triangle of a given measurement, follow these steps:
Draw a base BC\ =\ 12\ cm line segment.
Draw the ray BX and measure and draw \angle B\ =\ 90°.
Using a compass, determine that AB+AC = 18 cm.
Draw an arc at the point D on the ray BX with\ B\ as the center.
Join DC
Draw the perpendicular bisector of the line CD, with A\ as the intersection point.
Finally, join AC.
As a result, ABC is the necessary triangle. 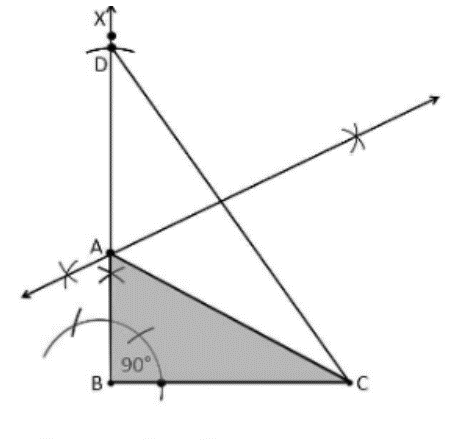
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out





