NCERT Solutions for Class 11 Math Chapter 7 Permutations and Combinations

Exercise 7.1

1. How many 3-digit numbers can be formed from the digits 1, 2, 3, 4 and 5 assuming that
(i) Repetition of the digits is allowed?
(ii) Repetition of the digits is not allowed?
Solution:
(i) Let us consider the 3-digit number ABC, with C representing the units, B representing the tens, and A representing the hundreds.
Now when repetition is permitted,
The maximum number of digits that can be used in C is 5. Since repetition is allowed, the maximum number of digits at B and A is also five.
As a result, the total number possible 3-digit numbers =5\ \times\ 5\ \times\ 5\ =125

(ii) Let us consider the 3-digit number ABC, with C representing the units, B representing the tens, and A representing the hundreds.
Now when repetition is not permitted,
The maximum number of digits that can be used in C is 5. Now let us assume one of the 5 digits is in place C; because repetition is not permitted, the number of possible digits for place B is limited to 4, and the number of possible digits for place A is limited to 3.
As a result, the total number of possible 3-digit numbers =5\ \times\ 4\ \times\ 3=60

2. How many 3-digits even numbers can be formed from the digits 1, 2, 3, 4, 5, 6 if the digits can be repeated?
Solution: Let us consider the 3-digit number ABC, with C representing the units, B representing the tens, and A representing the hundreds.
Because the number has to be even, the only digits that can be used at C are 2, 4, or 6. At C, the number of possible digits is 3.
So now repetition is permissible, the maximum number of digits that can be inserted at B is 6. Similarly, the maximum number of digits at A is 6.
As a result, the total number possible 3 digit numbers =\ 6\ \times\ 6\ \times\ 3\ =\ 108

3. How many 4-letter code can be formed using the first 10 letters of the English alphabet, if no letter can be repeated?
Solution:
Let’s suppose the four-digit code is 1234.
To begin with, there are a total of 10 letters available.
Assume that one of the ten is in the first position.
Now, as the repetition is no longer permitted, the number of letters possible at place 2 is 9. At 1 and 2, any 2 of the 10 alphabets can now be taken. The number of alphabets available for place 3 is 8, and the number of alphabets available for place 4 is 7.
As a result, the total number of 4 letter codes \ =10\ \times\ 9\ \times\ 8\ \times\ 7=5040 .

4. How many 5-digit telephone numbers can be constructed using the digits 0 to 9 if each number starts with 67 and no digit appears more than once?
Solution:
Let’s consider that ABCDE for the five-digit number. Given that each number’s first two digits are 67. As a result, the code is 67CDE.
The numbers available for place C are 0, 1,2,3,4,5,8,9, because repetition is not possible and 6 and 7 have already been taken. At place C, there are 8 possible digits. If one of them is taken at C, the number of digits that can be used at D is now 7. Similarly, the number of digits that can be used at E is 6.
As a result, the total five-digit numbers with given conditions =\ 8\ \times\ 7\ \times\ 6\ =\ 336 .

5. A coin is tossed 3 times and the outcomes are recorded. How many possible outcomes are there?
Solution:
It is provided that a coin will be tossed 3 times and the results will be recorded.
Heads and tails are the two possible outcomes of a coin toss.
At each coin toss, there are 2 possible outcomes.
As a result, the total number of possible outcomes after 3 times =\ 2\ \times\ 2\ \times\ 2\ =\ 8 .

6. Given 5 flags of different colours, how many different signals can be generated if each signal requires the use of 2 flags, one below the other?
Solution:
It is given 5 different colored flags.
We know that the signal requires the use of two flags.
The maximum number of flags that can be used for the upper flag is 5.
Now that one of the flags has been taken, there are only 4 flags left for the lower flag in the signal.
As a result, the number of ways in which signal can be given =\ 5\ \times\ 4\ =\ 20 .

Exercise 7.2

1. Evaluate
(i) \mathbf{8}!
(ii) \mathbf{4}!\ – 3!
Solution:
(i) We are given 8!
As we know that 8!\ =\ 8\ \times\ 7\ \times\ 6\ \times\ 5\ \times\ 4\ \times\ 3\ \times\ 2\ \times\ 1=\ 40320
(ii) We are given 4!-3!
4!-3!\ =\ (4\ \times\ 3!)\ – 3!
Above equation can be expressed as
=\ 3!\ (4-1)\\ =\ 3\ \times\ 2\ \times\ 1\ \times\ 3\\ =\ 18

2. Is \mathbf{3}!\ +\ \mathbf{4}!\ =\ \mathbf{7}! ?
Solution:
First, we will consider LHS 3!\ +\ 4!
Now we will calculate left hand side, we get
3!\ +\ 4!\ =\ (3\ \times\ 2\ \times\ 1)\ +\ (4\ \times\ 3\ \times\ 2\ \times\ 1)\\ =\ 6\ +\ 24\\ =\ 30
Consider RHS and the computing we obtain.
7!\ =\ 7\ \times\ 6\ \times\ 5\ \times\ 4\ \times\ 3\ \times\ 2\ \times\ 1\ =\ 5040
Thus, we get LHS\ \neq\ RHS
As a result, 3!\ +\ 4!\ \neq\ 7!

3. Compute
\frac{\mathbf{8}!}{\mathbf{6}!\times\mathbf{2}!}
Solution:
It is given that \frac{8!}{6!\times2!}
By separating all of the factorials and simplifying them, we get
\frac{8!}{6!\times2!}=\frac{8\times7\times6!}{6!\times2\times1} \\ \frac{8!}{6!\times2!}=\frac{8\times7}{2}=28

4. If \frac{\mathbf{1}}{\mathbf{6}!}+\frac{\mathbf{1}}{\mathbf{7}!}=\frac{ {x}}{\mathbf{8}!} find x.
Solution:
First, we will consider LHS, we get
\frac{1}{6!}+\frac{1}{7!}=\frac{1}{6!}+\frac{1}{7\times6!}\\ \Rightarrow\frac{7+1}{7\times6!}=\frac{8}{7!}
Now we will equate LHS and RHS, we get
\frac{8}{7!}=\frac{x}{8!}\\ \frac{8}{7!}=\frac{x}{8\times7!}
After rearranging, we get
8\times8=x\\ x=64

5. Evaluate
\frac{ {n}!}{\left( {n}- {r}\right)!} ,
When
(i) {n}\ =\ \mathbf{6},\ {r}\ =\ \mathbf{2}
(ii) {n}\ =\ \mathbf{9},\ {r}\ =\ \mathbf{5}
Solution:
(i) The given values are n\ =\ 6,\ r\ =\ 2
After substituting the values of n and r, we get
\frac{6!}{\left(6-2\right)!}=\frac{6\times5\times4!}{4!}=6\times5=30

(ii) The given values are n\ =\ 9,\ r\ =\ 5
After substituting the values of n and r, we get
\frac{9!}{\left(9-5\right)!}=\frac{9\times8\times7\times6\times5\times4!}{4!}=9\times8\times7\times6\times5=15120

Exercise 7.3

1. How many 3-digit numbers can be formed by using the digits 1 to 9 if no digit is repeated?
Solution:
There are a total of 9 digits given for selection.
The number of places where a digit has to be taken is 3.
Because no repetition is allowed, we get
\Rightarrow No.\ of\ permutations\={_3^9}P\=\frac{9!}{\left(9-3\right)!}=\frac{9!}{6!}=\frac{9\times8\times7\times6!}{6!}=504
As a result, there are 504 needed 3-digit numbers.

2. How many 4-digit numbers are there with no digit repeated?
Solution:
To discover a 4 number (digits does not repeat)
We will now have 4 places to put 4 digits.
So, because 0 cannot be at thousand’s place, there are 9 ways = 9 ways.
At the hundredth place = There are 9 digits to fill because 1 digit has already been taken = 9 ways
At the ten’s place = There are 8 digits to fill because 2 digit has already been taken = 8 ways
At the unit’s place = There are 7 digits that can be filled = 7 ways
The total number of ways to fill the four places =\ 9\ \times\ 9\ \times\ 8\ \times\ 7\ =\ 4536\ ways .
So there is a total of 4536 four-digit numbers, with no digits repeated.

3. How many 3-digit even numbers can be made using the digits 1, 2, 3, 4, 6, 7, if no digit is repeated?
Solution:
Even numbers indicate that the last digit should also be even.
The number of possible digits at one’s location is 3 (2, 4 and 6)
\Rightarrow No.of\ permutations={_1^3}P=\frac{3!}{\left(3-1\right)!}=\frac{3!}{2!}=3
One of the numbers is taken at one’s place, with a total of 5 possible digits.
\Rightarrow No.of\ permutations={_2^5}P=\frac{5!}{\left(5-2\right)!}=\frac{5!}{3!}=\frac{5\times4\times3!}{3!}=20
As a result, the total number of permutations =3\ \times\ 20=60

4. Find the number of 4-digit numbers that can be formed using the digits 1, 2, 3, 4, 5 if no digit is repeated. How many of these will be even?
Solution:
Total number of digits available for selection \ =\ 5
The number of places where a digit have to be taken =\ 4
As there is no repetition is permitted,
⇒ Number of permutations ={_4^5}P=\frac{5!}{\left(5-4\right)!}=\frac{5!}{1!}=120
When 2 and 4 are available, the number will be even.
The possibility of (2, 4) occurring at one’s place =\frac{\ 2}{5}\ =\ 0.4
The total number of even numbers =\ 120\ \times\ 0.4\ =\ 48

5. From a committee of 8 persons, in how many ways can we choose a chairman and a vice chairman assuming one person cannot hold more than one position?
Solution:
The total number of people in committee =\ 8
Number of positions to be filled =\ 2
⇒ Number of permutations ={_2^8}P=\frac{8!}{\left(8-2\right)!}=\frac{8!}{6!}=56

6. Find n if {_\mathbf{3}^{ {n}-\mathbf{1}}} {P}:{_\mathbf{4}^ {n}} {P}=\mathbf{1}:\mathbf{9} .
Solution:
The given equation can be written as
\frac{{_3^{n-1}}P}{{_4^n}P}=\frac{1}{9}\\ \frac{\left[\frac{\left(n-1\right)!}{\left(n-1-3\right)!}\right]}{\left[\frac{n!}{\left(n-4\right)!}\right]}=\frac{1}{9}\\ \frac{\left(n-1\right)!}{\left(n-4\right)!}\times\frac{\left(n-4\right)!}{n!}=\frac{1}{9}\\ \frac{\left(n-1\right)!}{n\left(n-1\right)!}=\frac{1}{9}\\ \frac{1}{n}=\frac{1}{9}\\ n=9

7. Find r if
(i) {_ {r}^\mathbf{5}} {P}=\mathbf{2}{_ {r}-\mathbf{1}^\mathbf{6}} {P}
(ii) {_ {r}^\mathbf{5}} {P}={_ {r}-\mathbf{1}^\mathbf{6}} {P}
Solution:
(i) It is given that {_r^5}P=2{_r-1^6}P
The given equation can be written as
\frac{5!}{\left(5-r\right)!}=2\times\frac{6!}{\left(6-r+1\right)!}\\ \frac{5!}{\left(5-r\right)!}=\frac{2\times6!}{\left(7-r\right)!}\\ \frac{5!}{\left(5-r\right)!}=\frac{2\times6\times5!}{\left(7-r\right)\left(6-r\right)\left(5-r\right)!}\\ 1=\frac{12}{\left(7-r\right)\left(6-r\right)}
After simplification, we get
\left(7-r\right)\left(6-r\right)=2\left(6\right)\\ 42-13r+r^2=12\\ r^2-13r+30=0\\ r^2-10r-3r+30=0\\ r\left(r-10\right)-3\left(r-10\right)=0\\ \left(r-3\right)\left(r-10\right)=0\\ r=3\ or\ r=10
But r=10 is not acceptable because in {_r^5}P , r cannot be higher than 5.
Thus, r=3

(ii) It is given that {_r^5}P={_r-1^6}P
The given equation can be written as
\frac{5!}{\left(5-r\right)!}=\frac{6!}{\left(7-r\right)!}\\ \frac{\left(7-r\right)!}{\left(5-r\right)!}=\frac{6!}{5!}\\ \frac{\left(7-r\right)\times\left(6-r\right)\times\left(5-r\right)!}{\left(5-r\right)!}=\frac{6\times5!}{5!}
After simplification, we get
\left(7-r\right)\times\left(6-r\right)=6\\ 42-7r-6r+r^2=6\\ r^2-13r+36=0\\ r^2-9r-4r+36=0\\ r\left(r-9\right)-4\left(r-9\right)=0\\ \left(r-4\right)\left(r-9\right)=0\\ r=4\ \ or\ \ r=9
But r=9 is not acceptable because in {_r^5}P , r cannot be higher than 5. Thus, r=4
8. How many words, with or without meaning, can be formed using all the letters of the word EQUATION, using each letter exactly once?
Solution:
The total number of different letters in EQUATION =\ 8
The number of letters that will be used to create a word =\ 8
⇒ Number of permutations ={_8^8}P=\frac{8!}{\left(8-8\right)!}=\frac{8!}{0!}=40320

9. How many words, with or without meaning can be made from the letters of the word MONDAY, assuming that no letter is repeated, if.
(i) 4 letters are used at a time,
(ii) All letters are used at a time,
(iii) all letters are used but first letter is a vowel?
Solution:
(i) Number of letters to be used is 4
⇒ Number of permutations ={_4^6}P=\frac{6!}{\left(6-4\right)!}=\frac{6!}{2!}=360

(ii) Number of letters to be used is 6
⇒ Number of permutations ={_6^6}P=\frac{6!}{\left(6-6\right)!}=\frac{6!}{0!}=720

(iii) Number of vowels in MONDAY = 2 (O and A)
⇒ Number of permutations in vowel ={_1^2}P=\frac{2!}{\left(2-1\right)!}=\frac{2!}{1!}=2
Now, we have 5 remaining places and 5 remaining letters to be used
⇒ Number of permutations ={_5^5}P=\frac{5!}{\left(5-5\right)!}=\frac{5!}{0!}=120
As a result, the total number of permutations =\ 2\ \times\ 120\ =240

10. In how many of the distinct permutations of the letters in MISSISSIPPI do the four I’s not come together?
Solution: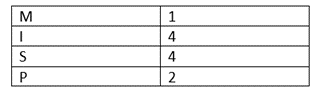
MISSISSIPPI has a total of 11 letters.
Letter Number of occurrence

⇒ Number of permutations =\frac{11!}{1!4!4!2!}=34650
When 4 I’s are grouped together, they are considered as a single letter.
∴ Total number of letters \ =11\ – 4 + 1 = 8
⇒ Number of permutations =\frac{8!}{1!\ 4!\ 2!}=840
As a result, the total number of permutations in which 4 I’s do not combine is
34650-840=33810 .

11. In how many ways can the letters of the word PERMUTATIONS be arranged if the
(i) Words start with P and end with S,
(ii) Vowels are all together,
(iii) There are always 4 letters between P and S?
Solution:
(i) PERMUTATIONS has a total of 12 letters.
T is the only letter that appears twice.
The letters P and S are fixed as the word’s first and last letters, respectively.
Number of letters remaining =12\ – 2 = 10
⇒ Number of permutations =\frac{{_10^{10}}P}{\ 2!}=\frac{10!}{2(10-10)!}=\frac{10!}{2}=1814400

(ii) The total number of vowels in PERMUTATIONS word are 5 (E, U, A, I, O)
Now, we will consider all the vowels together as one.
Number of permutations of vowels =\ 120
Now, the total number of letters =\ 12\ – 5 + 1= 8
⇒ Number of permutations =\frac{{_8^8}P}{\ 2!}=\frac{8!}{2(8-8)!}=\frac{8!}{2}=20160
As a result, the total number of permutations =\ 120\ \times\ 20160\ =\ 2419200

(iii) Number of places are as 1 2 3 4 5 6 7 8 9 10 11 12
Between the letters P and S, there should always be 4 letters.
1 and 6, 2 and 7, 3 and 8, 4 and 9, 5 and 10, 6 and 11, 7 and 12 are possible P and S places.
There are 7 possible ways.
Also, P and S can be interchanged,
No. of permutations =2\ \times\ 7\ =14
The remaining 10 places can be filled with any of the other 10 letters.
∴ No. of permutations =\frac{{_10^{10}}P}{\ 2!}=\frac{10!}{2(10-10)!}=\frac{10!}{2}=1814400
As a result, the total number of permutations is =\ 14\ \times\ 1814400\ =25401600 .

Exercise 7.4

1. If {_\mathbf{8}^ {n}} {C}={_\mathbf{2}^ {n}} {C} , find {_\mathbf{2}^ {n}} {C} .
Solution:
It is known that, if {_a^n}C={_b^n}C , then either a=b\ \ or\ n=a+b
Here, we have {_8^n}C={_2^n}C
So, we get
8=n-2\\ n=10
Now we will find the value of {_2^n}C
{_2^n}C={_2^{10}}C\\ \ \ \ \ \ \ \ =\frac{10!}{2!\left(10-2\right)!}\\ \ \ \ \ \ \ =\frac{10!}{2!\times8!}\\ \ \ \ \ \ \ =\frac{10\times9\times8!}{2\times1\times8!}\\ \ \ \ \ \ \ =45

2. Determine n if
(i) {_\mathbf{3}^{\mathbf{2} {n}}} {C}:{_\mathbf{3}^ {n}} {C}=\mathbf{12}:\mathbf{1}
(ii) {_\mathbf{3}^{\mathbf{2} {n}}} {C}:{_\mathbf{3}^ {n}} {C}=\mathbf{11}:\mathbf{1}
Solution:
(i) {_3^{2n}}C:{_3^n}C=12:1
The given equation can be written as
\frac{{_3^{2n}}C}{{_3^n}C}=\frac{12}{1}\\ \frac{\left(2n\right)!}{3!\left(2n-3\right)!}\times\frac{3!\left(n-3\right)!}{n!}=12\\ \frac{\left(2n\right)\left(2n-1\right)\left(2n-2\right)\left(2n-3\right)!}{\left(2n-3\right)!}\times\frac{\left(n-3\right)!}{n\left(n-1\right)\left(n-2\right)\left(n-3\right)!}=12\\ \frac{2\left(2n-1\right)\left(2n-2\right)}{\left(n-1\right)\left(n-2\right)}=12\\ \frac{2\left(2n-1\right)\left(2n-2\right)}{\left(n-1\right)\left(n-2\right)}=12\\ \frac{4\left(2n-1\right)\left(n-1\right)}{\left(n-1\right)\left(n-2\right)}=12\\ \frac{\left(2n-1\right)}{\left(n-2\right)}=\frac{12}{4}\\ \frac{\left(2n-1\right)}{\left(n-2\right)}=3\\ \left(2n-1\right)=3\left(n-2\right)\\ \left(2n-1\right)=3n-6\\ 2n-3n-1+6=0\\ -n+5=0\\ n=5

(ii) {_3^{2n}}C:{_3^n}C=11:1
The given equation can be written as
\frac{{_3^{2n}}C}{{_3^n}C}=\frac{11}{1}\\ \frac{\left(2n\right)!}{3!\left(2n-3\right)!}\times\frac{3!\left(n-3\right)!}{n!}=11\\ \frac{\left(2n\right)\left(2n-1\right)\left(2n-2\right)\left(2n-3\right)!}{\left(2n-3\right)!}\times\frac{\left(n-3\right)!}{n\left(n-1\right)\left(n-2\right)\left(n-3\right)!}=11\\ \frac{2\left(2n-1\right)\left(2n-2\right)}{\left(n-1\right)\left(n-2\right)}=11\\ \frac{2\left(2n-1\right)\left(2n-2\right)}{\left(n-1\right)\left(n-2\right)}=11\\ \frac{4\left(2n-1\right)\left(n-1\right)}{\left(n-1\right)\left(n-2\right)}=11\\ \frac{\left(2n-1\right)}{\left(n-2\right)}=\frac{11}{4}\\ \frac{4\left(2n-1\right)}{11\left(n-2\right)}=1\\ 4\left(2n-1\right)=11\left(n-2\right)\\ 8n-4=11n-22\\ 8n-11n-4+22=0\\ -3n+18=0\\ n=\frac{18}{3}\\ n=6

3. How many chords can be drawn through 21 points on a circle?
Solution:
It is given that there are 21 points on a circle.
As we know that we need two points on the circle to draw a chord
Thus, the number of chords is,
{_2^{21}}C=\frac{21!}{2!\left(21-2\right)!}\\ \ \ \ \ \ \ \ \ =\frac{21!}{2!19!}\\ \ \ \ \ \ \ \ \ =\frac{21\times20}{2}\\ \ \ \ \ \ \ \ \ =210
As a result, the total number of chords can be drawn are 210.

4. In how many ways can a team of 3 boys and 3 girls be selected from 5 boys and 4 girls?
Solution:
It is given that a team of 3 boys and 3 girls is to be selected from 5 boys and 4 girls.
We can select 3 boys from 5 boys in 5C3 ways
Similarly, we can select 3 boys from 54 girls in 4C3 ways
∴ Number of ways a team of 3 boys and 3 girls can be selected is 5C3 × 4C3
{_3^5}C\times{_3^4}C=\frac{5!}{3!2!}\times\frac{4!}{3!1!}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{5\times4\times3!}{3!\times2\times1}\times\frac{4\times3!}{3!\times1}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =10\times4\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =40

5. Find the number of ways of selecting 9 balls from 6 red balls, 5 white balls and 5 blue balls if each selection consists of 3 balls of each colour.

Solution:
There is total of 6 red balls, 5 white balls and 5 blue balls.
9 balls have to be selected in such a way that each selection consists of 3 balls of each colour.
We can select 3 red balls from 6 red balls in 6C3 ways
Similarly, we can select 3 white balls from 5 white balls in 5C3 ways
Similarly, we can select 3 blue balls from 5 blue balls in 5C3 ways
∴ Number of ways of selecting 9 balls is 6C3 ×5C3 × 5C3
{_3^6}C\times{_3^5}C\times{_3^5}C=\frac{6!}{3!3!}\times\frac{5!}{3!2!}\times\frac{5!}{3!2!}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{6\times5\times4\times3!}{3!\times3\times2}\times\frac{5\times4\times3!}{3!\times2\times1}\times\frac{5\times4\times3!}{3!\times2\times1}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =20\times10\times10\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =2000
As a result, the total number of ways of selecting 9 balls from 6 red balls, 5 white balls and 5 blue balls when each selection consists of 3 balls of each colour is 2000.

6. Determine the number of 5 card combinations out of a deck of 52 cards if there is exactly one ace in each combination.
Solution:
There are four aces in a deck of 52 cards. It’s essential to make a 5 combination with exactly one ace.
According to the question, we have to choose 1 Ace card from the 4 Ace cards.
The number of ways to choose 1 Ace from 4 Ace cards is 4C1.
Now choose 4 from a deck of 48 cards (52 cards – 4 Ace cards).
The number of ways to choose 4 cards from 48 cards is 48C4.
{_4^{48}}C\times{_1^4}C=\frac{48!}{4!44!}\times\frac{4!}{1!3!}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{48\times47\times46\times45\times44!}{4!44!}\times\frac{4!}{1!3!}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{48\times47\times46\times45}{3\times2}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{4669920}{6}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =778320

7. In how many ways can one select a cricket team of eleven from 17 players in which only 5 players can bowl if each cricket team of 11 must include exactly 4 bowlers?
Solution:
It is given that 17 players in which only 5 players can bowl if each cricket team of 11 must include exactly 4 bowlers
In a team of 11, we can use 4 bowlers because there are 5 players that can bowl.
The numbers of ways in which bowlers can be selected are 5C4
Other left players are =\ 17\ – 5(bowlers) = 12
Since we require 11 players in a team and have already chosen 4 bowlers, we have to choose 7 more from a group of 12.
∴ Number of ways we can select these players are: 12C7
∴ Total numbers of combinations possible are: 5C4 × 12C7
{_4^5}C\times{_7^{12}}C=\frac{5!}{4!1!}\times\frac{12!}{7!5!}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{12\times11\times10\times9\times8\times7!}{4\times3\times2\times1\times7!}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =3960
As a result, there are 3960 different ways to choose a team of 11 players, 4 of whom are bowlers, from a total of 17 players.

8. A bag contains 5 black and 6 red balls. Determine the number of ways in which 2 black and 3 red balls can be selected.
Solution:
In this question, a bag contains 5 black and 6 red balls
The total numbers of ways we can select 2 black balls from 5 black balls are 5C2
The total numbers of ways we can select 3 red balls from 6 red balls are 6C3
The total numbers of ways 2 black and 3 red balls can be selected are 5C2× 6C3
{_2^5}C\times{_3^6}C=\frac{5!}{2!3!}\times\frac{6!}{3!3!}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{5\times4\times3!}{2!\times3!}\times\frac{6\times5\times4\times3!}{3!\times3!}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{20}{2}\times\frac{120}{6}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =10\times20\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =200
As a result, there are 200 different ways select 2 black and 3 red balls from 5 black and 6 red balls.

9. In how many ways can a student choose a programme of 5 courses if 9 courses are available and 2 specific courses are compulsory for every student?
Solution:
In this question, 9 courses are available and 2 specific courses are compulsory for every student
Here, 2 of the 9 courses are required, thus a student must choose 2 of them 5\ – 2 = 3 courses
The total number of ways in which 3 ways can be selected from 9 – 2(compulsory courses) = 7 are 7C3
{_3^7}C=\frac{7!}{3!\left(7-3\right)!}\\ \ \ \ \ \ \ =\frac{7!}{3!\times4!} \ \ \ \ \ \ =\frac{7\times6\times5\times4!}{3!\times4!}\\ \ \ \ \ \ \ =\frac{210}{6}\\ \ \ \ \ \ \ =35
As a result, there are 35 different ways for a student select 5 courses from a total of 9 courses, with 2 of them being compulsory.

Miscellaneous Exercise

1. How many words, with or without meaning, each of 2 vowels and 3 consonants can be formed from the letters of the word DAUGHTER?
Solution:
DAUGHTER is made up of 3 vowels (A, E, and U) and 5 consonants (D, G, H, T, and R).
The three vowels can be chosen in 3C2 as only two vowels are to be chosen.
In the same way, the five consonants can be chosen in 5C3 different ways.
∴ The total number of vowels and consonants to choose would be 3C2 ×5C3
{_2^3}C\times{_3^5}C=\frac{3!}{2!\left(3-2\right)!}\times\frac{5!}{3!\left(5-3\right)!}=\frac{3!}{2!1!}\times\frac{5!}{3!2!}=30
Thus, the total number of ways is 30.
Each of these five letters can be arranged in five different ways to form a number of words
{_5^5}P=\frac{5!}{\left(5-5\right)!}=\frac{5!}{0!}=\frac{5!}{1}=5\times4\times3\times2\times1=120
Total amount of words formed: 30\ \times\ 120\ =\ 3600

2. How many words, with or without meaning, can be formed using all the letters of the word EQUATION at a time so that the vowels and consonants occur together?
Solution:
There are five vowels (A, E, I, O, U) and three consonants in the word EQUATION (Q, T, N)
There are 5C5 different ways to arrange 5 vowels.
\Rightarrow\frac{5!}{\left(5-5\right)!}=\frac{5\times4\times3\times2\times1}{0!}=\frac{120}{1}=120\ \ \ldots\ldots\ldots\ldots\ldots(1)
Similarly, the number of ways to arrange 3 consonants is 3P3.
\Rightarrow\frac{3!}{\left(3-3\right)!}=\frac{3\times2\times1}{0!}=\frac{6}{1}=6\ \ \ldots\ldots\ldots\ldots\ldots(2)
Vowels and consonants can appear together in two different ways (AEIOU) (QTN) or (QTN) (AEIOU).
There are a total of 2\times{_5^5}C\times{_3^3}C\ ways for a vowel and a consonant to occur together.
2\times120\times6=1440\

3. A committee of 7 has to be formed from 9 boys and 4 girls. In how many ways can this be done when the committee consists of:
(i) Exactly 3 girls?
(ii) At least 3 girls?
(iii) At most 3 girls?
Solution:
(i) We are given exactly 3 girls
The total number of females is 4.
3 are to be chosen from the group.
Thus, the total number of choices for making a choice is 4C3.
The numbers of boys are 9 out of which 4 are to be chosen which is given by 9C4
Total ways of forming the committee with exactly three girls = 4C3 × 9C4
{_3^4}C\times{_4^9}C=\frac{4!}{3!\left(4-3\right)!}\times\frac{9!}{4!\left(9-4\right)!}=\frac{4!}{3!1!}\times\frac{9!}{4!5!}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{9\times8\times7\times6\times5\times4\times3\times2\times1}{3\times2\times1\times5\times4\times3\times2\times1}=504

(ii) We are given at least 3 girls
There are two ways to form a committee, both of which require at least three girls.
There are 3 girls and 4 boys or there are 4 girls and 3 boys
We have chosen three girls from part (i)
4C4 methods would be used to choose 4 girls and three boys.
And choosing 3 boys would be done in 9C3
Total ways = 4C4 × 9C3
{_4^4}C\times{_3^9}C=\frac{4!}{4!\left(4-4\right)!}\times\frac{9!}{3!\left(9-3\right)!}=\frac{4!}{4!0!}\times\frac{9!}{3!6!}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{9\times8\times7\times6!}{3\times2\times1\times6!}=84
The total number of ways to form the committee is 504\ +\ 84\ =\ 588

(iii) Since at most 3 girls are to be there in every committee, the committee can consist of 3 girls and 4 boys, 2 girls and 5 boys, 1 girl and 6 boys and no girl and 7 boys
In this case the numbers of possibilities are
3 girls and 4 boys can be selected in 4C3 × 9C4 ways
2 girls and 5 boys can be selected in 4C2 × 9C5 ways
1 girl and 6 boys can be selected in 4C1 × 9C6 ways
No girl and 7 boys can be selected in 4C0 × 9C7 ways
As a result, the required number of ways in this case is
{_3^4}C\times{_4^9}C+{_2^4}C\times{_5^9}C+{_1^4}C\times{_6^9}C+{_0^4}C\times{_7^9}C=\frac{4!}{3!1!}\times\frac{9!}{4!5!}+\frac{4!}{2!2!}\times\frac{9!}{5!4!}+\frac{4!}{1!3!}\times\frac{9!}{6!3!}+\frac{4!}{0!4!}\times\frac{9!}{7!2!}\ \ \ \\ =504+756+336+36 =1632

4. If the different permutations of all the letter of the word EXAMINATION are listed as in a dictionary, how many words are there in this list before the first word starting with E?
Solution:
There are 11 letters in the word EXAMINATION, with A, I, and N occurring two times and all other letters occurring only once.
Those words that begin with the letter A will be listed before those that begin with the letter E in a dictionary.
As a result, to find the number of words beginning with A, the letter A is fixed towards the far left, and the following 10 letters are rearranged one at a time.
Since there are 2 Is and 2 Ns in the remaining 10 letters
The number of words begins with A A=\frac{10!}{2!2!}=907200
As a result, the required numbers of words are 907200.

5. How many 6-digit numbers can be formed from the digits 0, 1, 3, 5, 7 and 9 which are divisible by 10 and no digit is repeated?
Solution:
If the unit place has a 0 in it, the number is divisible by 10.
The 6-digit number must be created, with the unit place set to 0.
1, 3, 5, 7, and 9 can fill the remaining 5 places.
Here, n\ =\ 5
And the numbers of choice available are 5
So there are a total of 5P5 ways to fill the remaining spots.
=\frac{5!}{\left(5-5\right)!}\times1=\frac{5!}{1}\times1=5\times4\times3\times2\times1\times1=120

6. The English alphabet has 5 vowels and 21 consonants. How many words with two different vowels and 2 different consonants can be formed from the alphabet?
Solution:
We know that the English alphabet contains 5 vowels and 21 consonants.
Selecting two vowels from a list of 5 is done in 5C2 ways.
Selecting two consonants from a list of 21 is done in 21C2 ways.
The total number of possible combinations using two vowels and 2 consonants is 5C2 × 21C2
\Rightarrow\frac{5!}{2!\ 3!}\times\frac{21!}{2!\ 19!}=\frac{5\times4\times3!}{2!3!}\times\frac{21\times20\times19!}{2\times1\times19!}=2100
These four letters can be arranged in four different ways i.e., 4P4
\frac{4!}{0!}=4\times3\times2\times1=24ways
The total number of possible words is 24\ \times\ 2100\ =\ 50400

7. In an examination, a question paper consists of 12 questions divided into two parts i.e., Part I and Part II, containing 5 and 7 questions, respectively. A student is required to attempt 8 questions in all, selecting at least 3 from each part. In how many ways can a student select the questions?
Solution:
The question paper is broken into two parts, with Part I including 5 questions and Part II containing 7 questions, respectively.
A student must attempt 8 questions, at least three from each part.
This can be done in one of 3 ways:
(i) 3 questions from part I and 5 questions from part II
(ii) 4 questions from part I and 4 questions from part II
(iii) 5 questions from part I and 3 questions from part II
Thus,
3 questions from Part I and 5 questions from Part II can be selected in 5C3 × 7C5 ways.
4 questions from Part I and 4 questions from Part II can be selected in 5C4 × 7C4 ways.
5 questions from Part I and 3 questions from Part II can be selected in 5C5 × 7C3 ways.
As a result, the required number of ways to select questions
{_3^5}C\times{_5^7}C+{_4^5}C\times{_4^7}C+{_5^5}C\times{_3^7}C=\frac{5!}{3!2!}\times\frac{7!}{5!2!}+\frac{5!}{4!1!}\times\frac{7!}{4!3!}+\frac{5!}{5!0!}\times\frac{7!}{3!4!}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =210+175+35 \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =420

8. Determine the number of 5-card combinations out of a deck of 52 cards if each selection of 5 cards has exactly one king.
Solution:
We have a deck of cards with 4 kings in it.
There are 52 cards left in the deck.
Ways of selecting a king from the deck is 4C1
Ways of selecting the remaining 4 cards from 48 cards is 48C4
The total number of selections for the five cards with one king is always 4C1 × 48C4
\frac{4!}{1!\ 3!}\times\frac{48!}{4!\ 44!}=\frac{4\times3!}{3!}\times\frac{48\times47\times46\times45\times44!}{4\times3\times2\times1\times44!}=778320

9. It is required to seat 5 men and 4 women in a row so that the women occupy the even places. How many such arrangements are possible?
Solution:
It is stated that there is a total of 9 people.
Women occupies even places that means they will be sitting on 2nd, 4th, 6th and 8th place while men will be sitting on 1st, 3rd, 5th,7th and 9th place.
4P4 is the number of women who can sit in four different places and ways.
\frac{4!}{\left(4-4\right)!}=\frac{4\times3\times2\times1}{0!}=24
If 5 men can occupy 5 seats in 5 different ways, the total number of possible seating arrangements is 5P5.
\frac{5!}{\left(5-5\right)!}=\frac{5\times4\times3\times2\times1}{1}=120
The total number of possible seating arrangement is 24\ \times\ 120\ =\ 2880

10. From a class of 25 students, 10 are to be chosen for an excursion party. There are 3 students who decide that either all of them will join or none of them will join. In how many ways can the excursion party be chosen?
Solution:
In this question we have 2 options:
(i) Either all 3 will go
The remaining students in class are: 25\ – 3 = 22
There are a total of 7 students who are to be chosen for the party.
The number of ways choosing the remaining 22 students is 22C7
\frac{22!}{7!15!}=170544

(ii) None of them will go
The number of students attending will be 10.
Students who are still eligible to attend = 22
There are 22C10 different ways in which these 10 students can be selected.
\frac{22!}{10!12!}=646646
The total number of ways students can be selected as 170544\ +\ 646646\ =\ 817190

11. In how many ways can the letters of the word ASSASSINATION be arranged so that all the S’s are together?
Solution:
There are four ‘S’ in the word ASSASSINATION. Because all 4 ‘S’ have to be arranged together, we’ll consider them as a unit.
3 ‘A’, 2 ‘I’, 2 ‘N’, T are the remaining letters
There are 9 letters to arrange (including four ‘S’).
By using the formula \frac{n!}{p_1!{\ p}_2!\ p_3!} , where n is number of terms and p1, p2, p3 are the number of times the repeating letters repeat themselves.
Here, we have p_1=3,\ p_2=2,\ p_3=2
Substituting the values in the formula, we get
\frac{10!}{3!2!2!}=\frac{10\times9\times8\times7\times6\times5\times4\times3!}{3!\times2\times2\times1\times1}=151200
As a result, there are 151200 required numbers of ways of arranging the letters of the given word.