NCERT Solutions Class 11 Maths Chapter 2- Relation And Function

Exercise 2.1

1. If \left ( \frac{x}{3}+1,y-\frac{2}{3}\right )=\left ( \frac{5}{3},\frac{1}{3} \right ), find the values of x and y.

Solution:
According to the given question,
\left ( \frac{x}{3}+1,y-\frac{2}{3}\right )=\left ( \frac{5}{3},\frac{1}{3} \right )
Since the given ordered pairs are equal, the corresponding elements will also be equal.
Hence,
\frac{x}{3}+1=\frac{5}{3}
and
y-\frac{2}{3}=\frac{1}{3}
Solving the above relations we get,
x+3=5\\ x=2
and

3y-2=1\\ 3y=3\\ y=1
Therefore the result is,
x=2 and
y=1

2. If the set A has 3 elements and the set B=\left\{ 3,4,5\right\} , then find the number of elements in \left ( A\times B \right ) ?
Solution:
According to the given question, there are 3 elements in set A and the elements in set B are B=\left\{ 3,4,5\right\} .
So, the number of elements in set B is also 3.
So, the number of elements in
\left ( A\times B \right )=\left ( \text{Number of elements in A} \right )\times \left ( \text{Number of elements in B} \right )\\ =3\times 3=9
Therefore, the result will be
\text{Number of elements in}\left ( A\times B \right )=3\times 3=9

3. If G=\left\{ 7,8\right\} and H=\left\{ 5,4,2\right\} find G\times H and H\times G .
Solution:
According to the given question, G=\left\{ 7,8\right\}
and H=\left\{ 5,4,2\right\}
We already know that,
The Cartesian product of two non-empty sets P and Q is given as
P\times Q=\left\{\left ( p,q \right ): p \epsilon P , q \epsilon Q \right\}
Hence,
G\times H=\left\{\left ( 7,5 \right ),\left ( 7,4 \right ),\left ( 7,2 \right )\left ( 8,5 \right ),\left ( 8,5 \right ),\left ( 8,4 \right ),\left ( 8,2 \right ) \right\}

4. State whether each of the following statements are true or false. If the statement is false, rewrite the given statement correctly.
(i) If P=\left\{ m,n\right\} and Q=\left\{ n,m\right\} , then P\times Q=\left\{\left ( m,n \right ),\left ( n,m \right )\right\} .
(ii) If A and B are non-empty sets, then A\times B is a non-empty set of ordered pairs \left ( x,y \right ) such that x\epsilon A and y\epsilon B .
(iii) If A=\left\{1,2 \right\},B=\left\{3,4 \right\} , then A\times \left ( B\cap \phi \right )=\phi .
Solution:
(i) This statement is False. The correct statement will be:
If P=\left\{ m,n\right\} and Q=\left\{ n,m\right\} , then
P\times Q=\left\{\left ( m,m \right ),\left ( m,n \right ),\left (n,m \right ),\left ( n,n \right )\right\}
(ii) True
(iii) True

5. If A=\left\{-1,1 \right\} , find A\times A\times A .
Solution:
The A\times A\times A for a non-empty set A can be calculated by:
A\times A\times A=\left\{\left ( a,b,c \right ):a,b,c\epsilon A \right\}
Here, according to the given question A=\left\{-1,1 \right\}
Therefore,
A\times A\times A=\left\{\left ( -1,-1,-1 \right ),\left ( -1,-1,1 \right ),\left ( -1,1,-1 \right ),\left ( -1,1,1 \right ),\left ( 1,-1,-1 \right ),\left ( 1,-1,1 \right ),\left ( 1,1,-1 \right ),\left ( 1,1,1 \right ) \right\}

6. If A\times B=\left\{\left ( a,x \right ),\left ( a,y \right ),\left ( b,x \right ),\left ( b,y \right ) \right\} . Find A and B.
Solution:
According to the given question,
A\times B=\left\{\left ( a,x \right ),\left ( a,y \right ),\left ( b,x \right ),\left ( b,y \right ) \right\}
We already know that the Cartesian product of two non-empty sets P and Q can be given as:
P\times Q=\left\{\left ( p,q \right ): p \epsilon P , q \epsilon Q \right\}

Hence, A is the set of first elements and B is the set of second elements.
Then, A=\left\{ a,b\right\}
and
B=\left\{ x,y\right\}

7. Let A=\left\{ 1,2\right\},B=\left\{ 1,2,3,4\right\},C=\left\{ 5,6\right\} and D=\left\{ 5,6,7,8\right\} . Verify that
(i) A\times \left ( B\cap C \right )=\left ( A\times C \right )
(ii) A\times C is a subset of B\times D
Solution:
According to the given question,
A=\left\{ 1,2\right\},B=\left\{ 1,2,3,4\right\},C=\left\{ 5,6\right\} and D=\left\{ 5,6,7,8\right\}
(i) To verify: A\times \left ( B\cap C \right )=\left ( A\times B \right )
We know, B\cap C=\left\{ 1,2,3,4\right\}\cap \left\{5,6 \right\}=\phi
Here,
\text{L.H.S.}=A\times \left ( B\cap C \right )=A\times \phi =\phi
Now,
A\times B=\left\{\left ( 1,1 \right ),\left ( 1,2 \right ),\left ( 1,3 \right ),\left ( 1,4 \right ),\left ( 2,1 \right ),\left ( 2,2 \right ),\left ( 2,3 \right ),\left ( 2,4 \right ) \right\}

A\times C=\left\{\left ( 1,5 \right ),\left ( 1,6 \right ),\left ( 2,5 \right ),\left ( 2,6 \right ) \right\}
Here,
\text{R.H.S.}=\left ( A\times B \right )\cap \left ( A\times C \right )=\phi
Hence, L.H.S. = R.H.S
Hence proved.
(ii) To verify: A\times C is a subset of B\times D
Here,
A\times C=\left\{ \left ( 1,5 \right ),\left ( 1,6 \right ),\left ( 2,5 \right ),\left ( 2,6 \right )\right\}
Also,
B\times D=\left\{ \left ( 1,5 \right ),\left ( 1,6 \right ),\left ( 1,7 \right ),\left ( 1,8 \right ),\left ( 2,5 \right ),\left ( 2,6 \right ),\left ( 2,8 \right ),\left ( 3,5 \right ),\left ( 3,6 \right ),\left ( 3,7 \right ),\left ( 3,8 \right ),\left ( 4,5 \right ),\left ( 4,6 \right ),\left ( 4,7 \right ),\left ( 4,8 \right )\right\}
Now, we can see that the elements of set A\times C are same as the elements of set B\times D .
Therefore, A\times C is a subset of B\times D .
– Hence proved.

8. Let A=\left\{ 1,2\right\} and B=\left\{ 3,4\right\} . Write A\times B . How many subsets will A\times B have? List them.
Solution:
According to the given question,
A=\left\{ 1,2\right\}
and
B=\left\{ 3,4\right\}
Hence,

We already know that,
\text{If C is a set with }n\left ( C \right )=m,\text{then } n[P\left ( C \right )]=2m
Hence, the set A\times B has 24 = 16 subsets.
Also, the subsets are mentioned below:
\phi,\left\{ \left ( 1,3 \right )\right\},\left\{ \left ( 1,4 \right )\right\},\left\{ \left ( 2,3 \right )\right\},\left\{ \left ( 2,4 \right )\right\},\left\{ \left ( 1,3 \right )\right\},\left\{ \left ( 1,4 \right )\right\},\left\{ \left ( 1,3 \right )\right\},\left\{ \left ( 2,3 \right )\right\},\left\{ \left ( 1,3 \right )\right\},\left\{ \left ( 2,4 \right )\right\},\left\{ \left ( 1,4 \right )\right\},\left\{ \left ( 2,3 \right )\right\},\left\{ \left ( 1,4 \right )\right\},\left\{ \left ( 2,4 \right )\right\},\left\{ \left ( 2,3 \right )\right\},\left\{ \left ( 2,4 \right )\right\},\left\{ \left ( 1,3 \right )\right\},\left\{ \left ( 1,4 \right )\right\},\left\{ \left ( 2,3 \right )\right\},\left\{ \left ( 1,3 \right )\right\},\left\{ \left ( 1,4 \right )\right\},\left\{ \left ( 2,4 \right )\right\},\left\{ \left ( 1,3 \right )\right\},\left\{ \left ( 2,3 \right )\right\},\left\{ \left ( 2,4 \right )\right\},\left\{ \left ( 1,4 \right )\right\},\left\{ \left ( 2,3 \right )\right\},\left\{ \left ( 2,4 \right )\right\}

9. Let A and B be two sets such that n\left ( A \right )=3 \text{ and } n\left ( B \right )=2 . If (x, 1), (y, 2), (z, 1) are in A × B, find A and B, where x, y and z are distinct elements.
Solution:
According to the question,

n\left ( A \right )=3 \text{ and } n\left ( B \right )=2;\text{ and }\left ( x,1 \right ),\left ( y,2 \right ),\left ( z,1 \right ) are in A\times B .
We already know that,
A=\text{Set of first elements of the of }A\times B B=\text{Set of second elements of the of }A\times B
So, we can say that x,y \text{ and }z are the elements of set A and 1,2 are the elements of set B.
n\left ( A \right )=3 \text{ and } n\left ( B \right )=2
Therefore,
set A=\left\{ x,y,z\right\}\text{ and }B=\left\{ 1,2\right\}

10. The Cartesian product A\times A has 9 elements among which are found \left ( -1,0 \right )\text{ and }\left ( 0,1 \right ) . Find the set A and the remaining elements of A\times A .
Solution:
We already know that,
n\left ( A \right )=p\text{ and }n\left ( B \right )=q,\text{then }n\left ( A\times B \right )=pq
Also, n\left ( A\times A \right )=n\left ( A \right )\times n\left ( A \right )
According to the given question,

n\left ( A\times A \right )=9\\ n\left ( A \right )\times n\left ( A \right )=9\\ n\left ( A \right )=3
Also According to the question, the ordered pairs \left ( -1,0\right )\text{ and }\left ( 0,1 \right ) are two of the nine elements of A\times A .
Also, A\times A=\left\{ \left ( a,a \right ):a\epsilon A\right\} .
Thus, –1, 0, and 1 should be the elements of A.
\text{As }n\left ( A \right )=3,\\ A=\left\{ -1,0,1\right\}
Hence, the rest elements of set A\times A are:
\left ( -1,-1\right ),\left ( -1,1 \right ),\left ( 0,-1 \right ),\left ( 0,0 \right ),\left ( 1,-1 \right ),\left ( 1,0 \right )\text{ and }\left ( 1,1 \right )

Exercise 2.2

1. Let A=\left\{ 1,2,3,4,56,,7,8,9…….14\right\} . Define a relation R from A to A by R=\left\{ \left ( x,y \right ): 3x-y=0,\text{ where }x,y\epsilon A\right\} . Write down its domain, codomain and range.
Solution:
According to the given question,
The relation R is given as:
R=\left\{ \left ( x,y \right ): 3x-y=0,\text{ where }x,y\epsilon A\right\}\\ =\left\{ \left ( x,y \right ): 3x=y,\text{ where }x,y\epsilon A\right\}

Hence,
R=\left\{ \left ( 1,3 \right ),\left ( 2,6 \right ),\left ( 3,9 \right ),\left ( 4,12 \right )\right\}
Now,
We can say that the domain of R is the set of all the first elements of the given relation.
\text{Domain of R}=\left\{ 1,2,3,4\right\}

The whole set A will be the codomain of relation R.
\text{Co-Domain of R}=A=\left\{ 1,2,3,4…….,14\right\}

The range of R will be the set of all second elements of the ordered pairs in the given relation.
\text{Range of R}=A=\left\{ 3,6,9,12\right\}

2. Define a relation R on the set N of natural numbers by R=\left\{ \left ( x,y \right ):y=x+5,\text{ x is a natural number less than 4; }x,y\epsilon N\right\}. Depict this relationship using roster form. Write down the domain and the range.

Solution:
The relation R is given as:
R=\left\{ \left ( x,y \right ):y=x+5,\text{ x is a natural number less than 4; }x,y\epsilon N\right\}
The natural numbers which are less than 4 will be 1,2 and 3.
Hence,
R=\left\{ \left ( 1,6 \right ),\left ( 2,7 \right ),\left ( 3,8 \right )\right\}

The domain of R will be the set of all first elements of the pairs in the relation R.
\text{Domain of R}=\left\{1,2,3\right\}

The range of R is the set of all second elements of the ordered pairs in the relation.
\text{Range of R}=\left\{6,7,8\right\}

3. A=\left\{ 1,2,3,5\right\} \text{ and }B=\left\{ 4,6,9\right\} . Define a relation R from A to B by R=\left\{ \left ( x,y \right ):\text{the difference between x and y is odd;}x\epsilon A,y\epsilon B\right\} . Write R in roster form.
Solution:
According to the given question,
A=\left\{ 1,2,3,5\right\} \text{ and }B=\left\{ 4,6,9\right\}
The relation from A to B is given by:

Therefore,
R=\left\{ \left ( 1,4 \right ),\left ( 1,6 \right ),\left ( 2,9 \right ),\left ( 3,4 \right ),\left ( 3,6 \right ),\left ( 5,4 \right ),\left ( 5,6 \right )\right\}

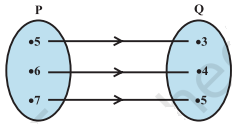
4. The figure shows a relationship between the sets P and Q. write this relation
(i) in set-builder form (ii) in roster form.
What is its domain and range?

Solution:
According to the given question,
P=\left\{ 5,6,7\right\},Q=\left\{ 3,4,5\right\}
The relation between P and Q will be :
Set-builder form
(i) R=\left\{ \left ( x,y \right ):y=x-2;x\epsilon P\right\} \text{ or }R=\left\{ \left ( x,y \right ):y=x-2 \text{ for }x=5,6,7\right\}
Roster form
(ii) R=\left\{ \left ( 5,3 \right ),\left ( 6,4 \right ),\left ( 7,5 \right )\right\} \text{Domain of R}=\left\{5,6,7 \right\}\\ \text{Range of R}=\left\{3,4,5 \right\}

5. Let A=\left\{ 1,2,3,4,5,6\right\}. Let R be the relation on A defined by\left\{ \left ( a,b \right ):a,b\epsilon A,\text{ b is exactly divisible by a}\right\}.
(i) Write R in roster form
(ii) Find the domain of R
(iii) Find the range of R.

Solution:
According to the given question,
A=\left\{ 1,2,3,4,5,6\right\}
and relation
R=\left\{ \left ( a,b \right ):a,b\epsilon A,\text{ b is exactly divisible by a}\right\}
Then,
(i) R=\left\{\left ( 1,1 \right ),\left ( 1,2 \right ),\left ( 1,3 \right ),\left ( 1,4 \right ),\left ( 1,6 \right ),\left ( 2,2 \right ),\left ( 2,4 \right ),\left ( 2,6 \right ),\left ( 3,3 \right ),\left ( 3,6 \right ),\left ( 4,4 \right ),\left ( 6,6 \right ) \right\}
(ii) \text{Domain of R}=\left\{ 1,2,3,4,6\right\}
(iii) \text{Range of R}=\left\{ 1,2,3,4,6\right\}

6. Determine the domain and range of the relation R defined by R=\left\{ \left ( x,x+5 \right ):x\epsilon \left\{ 0,1,2,3,4,5\right\}\right\}
Solution:
According to the given question,
Relation R = {(x, x + 5): x ∈ {0, 1, 2, 3, 4, 5}}
Thus,
R=\left\{ \left ( x,x+5 \right ):x\epsilon \left\{ 0,1,2,3,4,5\right\}\right\}

Therefore,
\text{Domain of R}=\left\{ 0,1,2,3,4,5\right\}\text{ and, }\\ \text{Range of R}=\left\{ 5,6,7,8,9,10\right\}

7. Write the relation R=\left\{ \left ( x,x^{3} \right ):\text{x is prime number less than 10}\right\}
in roster form.
Solution:
According to the question,
Relation
R=\left\{ \left ( x,x^{3} \right ):\text{x is prime number less than 10}\right\}
The prime numbers less than 10 will be 2, 3, 5, and 7.
Hence,
R=\left\{ \left ( 2,8 \right ),\left ( 3,27 \right ),\left ( 5,125 \right ),\left ( 7,343 \right )\right\}

8. Let A=\left\{ x,y,z\right\}\text{ and }B=\left\{ 1,2\right\} .Find the number of relations from A to B.
Solution:
According to the given question,
A=\left\{ x,y,z\right\}\text{ and }B=\left\{ 1,2\right\}.
So,
A\times B=\left\{ \left ( x,1 \right ),\left ( x,2 \right ),\left ( y,1 \right ),\left ( y,2 \right ),\left ( z,1 \right ),\left ( z,2 \right )\right\}
As n\left ( A\times B \right )=6,\text{ number of subsets of }A\times B=26
Therefore, the number of relations from A to B will be 26.

9. Let R be the relation on Z defined by R=\left\{ \left ( a,b \right ):a,b\epsilon Z,a-b\text{ is an integer}\right\}.
Find the domain and range of R.

Solution:
Given,
Relation R=\left\{ \left ( a,b \right ):a,b\epsilon Z,a-b\text{ is an integer}\right\}
We already know that the difference between any two integers will always be an integer.
Hence,
\text{Domain of R}=Z\text{ and Range of R}=Z

Exercise 2.3

1. Which of the following relations are functions? Give reasons. If it is a function, determine its domain and range.
(i) {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
(ii) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
(iii) {(1, 3), (1, 5), (2, 5)}
Solution:
(i) {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
As 2, 5, 8, 11, 14, and 17 are the elements of the domain of the given relation in the queation having their unique images, we can call this relation as a function.
Therefore,
\text{domain}=\left\{ 2,5,8,11,14,17\right\}\text{ and range}=\left\{ 1\right\}
(ii) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
As 2, 4, 6, 8, 10, 12, and 14 are the elements of the domain of the given relation in the queation having their unique images, we can call this relation as a function.
Therefore,

\text{domain}=\left\{ 2,4,6,8,10,12,14\right\}\text{ and range}=\left\{ 1,2,3,4,5,6,7\right\}
(iii) {(1, 3), (1, 5), (2, 5)}
It can be observed that the same first element, 1, corresponds to two different images, 3 and 5, indicating that this relation is not a function.

2. Find the domain and range of the following real function:
(i) f\left ( x \right )=-\left| x\right|(ii) f\left ( x \right )=\sqrt{\left ( 9-x^{2} \right )}

Solution:
(i) Given,
f\left ( x \right )=-\left| x\right|,x\epsilon R
We already know that,
\left| x\right|= x,x\geq 0\\ \left| x\right|= -x,x< 0\\ \therefore f\left ( x \right )=-\left| x\right|= -x,x\geq 0\\ \therefore f\left ( x \right )=-\left| x\right|= x,x< 0 \text{As}f\left ( x \right )\text{can be defined as }x\epsilon R,\text{domain of f}=R

We can also see that the range of f\left ( x \right )=-\left| x\right| will be all real numbers except positive real numbers.
Hence, the range of f will be (–∞, 0].
(ii) f\left ( x \right )=\sqrt{\left ( 9-x^{2} \right )}

\text{As }\sqrt{\left ( 9-x^{2} \right )},-3\leq x\leq 3,x\epsilon R\\ \text{for }9-x^{2}\geq 0
Hence,

\text{domain of }f\left ( x \right )=\left\{ x:-3\leq x\leq 3\right\}\text{ or }\left [ -3,3 \right ]
So,
For any value of x in [–3, 3], the value of f(x) will lie from 0 to 3.
Therefore,
\text{range of }f\left ( x \right )=\left\{ x:0\leq x\leq 3\right\}\text{ or }\left [ 0,3 \right ]

3. A function f is defined by f\left ( x\right )=2x-5. Write down the values of
(i) f(0), (ii) f(7), (iii) f(–3)

Solution:
According to the given question,
Function, f\left ( x\right )=2x-5 .
Therefore,
(i) f\left ( 0\right )=2\times 0-5=0-5=-5
(ii) f\left ( 7\right )=2\times 7-5=14-5=9
(iii) f\left ( -3\right )=2\times \left ( -3 \right )-5=-6-5=-11

4. The function ‘t’ which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by t\left ( C \right )=\frac{9C}{5}+32.Find (i) t(0) (ii) t(28) (iii) t(–10) (iv) The value of C, when t(C) = 212

Solution:
The given function in the question is,
t\left ( C \right )=\frac{9C}{5}+32
Hence,
t\left ( 0 \right )=\frac{9\times 0}{5}+32=0+32=32

(ii) t\left ( 28 \right )=\frac{9\times 28}{5}+\frac{252+160}{5}=\frac{412}{5}

(iii)
t\left ( -10 \right )=\frac{9\times\left ( -10 \right )}{5}+32=9\times \left ( -2 \right )+32=-18+32=14

(iv) According to the given question,
t\left ( C \right )=212\\ \therefore 212=\frac{9C}{5}+32\\ \frac{9C}{5}=212-32\\ \frac{9C}{5}=180\\ 9C=180\times 5\\ C=\frac{180\times 5}{9}=100\\ \text{Hence,the value of t while}t\left ( C \right )=212\text{ will be}=100

5. Find the range of each of the following functions.
(i) f\left ( x \right )=2-3x,x\epsilon R,x> 0
(ii) f\left ( x \right )=x^{2}+2,x\epsilon R
(iii) f\left ( x \right )=x,x\epsilon R

Solution:
(i) The given statement is,
f\left ( x \right )=2-3x,x\epsilon R,x> 0
The values of f(x) for the different values of x> 0 will be:
x
0.01
0.1
0.9
1
2
2.5
4
5
…
f(x)
1.97
1.7
-0.7
-1
-4
-5.5
-10
-13
…

We can see that the range of f is the set of all real numbers that are less than 2.
\text{Range of f}=\left ( -\infty,2 \right )

Now we have,
x> 0\\ \text{Hence,}\\ 3x> 0\\ -3x> 0\text{ [Multiplying by -1 on both sides,the inequality sign will change]}\\ 2-3x< 2
Hence,
\text{Value of }2-3x\text{will be less than 2}\\ \text{Range}=\left ( -\infty,2 \right )

(ii) According to the given statement,
f\left ( x \right )=x^{2}+2,x\epsilon R
The values of f(x) for the different values of x,x\epsilon R will be:
x
0
0.3
0.8
1
2
3
…
f(x)
2
2.09
2.64
3
6
11
…

We can see that the range of f is the set of all the real numbers that are greater than 2.
\text{Range of f}=[2,\infty)

We already know that,
x^{2}\geq 0\\ \text{then,}\\ x^{2}+2\geq 2\text{ [Adding 2 on both sides]}
Therefore,
\text{The value of of }x^{2}+2\text{ will be always greater than or equal to 2},x\epsilon R\\ \text{Range}=[2,\infty)

(iii) According to the given statement,
f\left ( x \right )=x,x\epsilon R
We can clearly see that, the range of f will be the set of all real numbers.
Therefore,
\text{Range of f}=R

Miscellaneous Exercise

1. The relation f is defined byf\left ( x \right )=\begin{Bmatrix}x^{2},0\leq x\leq 3 \\3x,3\leq x\leq 10\end{Bmatrix}
The relation g is defined byg\left ( x \right )=\begin{Bmatrix}x^{2},0\leq x\leq 2\\3x,2\leq x\leq 10\end{Bmatrix}

Show that f is a function and g is not a function.

Solution:
The given relation f is defined as:
f\left ( x \right )=\begin{Bmatrix} x^{2},0\leq x\leq 3 \\ 3x,3\leq x\leq 10 \end{Bmatrix}
We can see that,
\text{for }0\leq x< 3,\\ f\left ( x \right )=x^{2}\text{ and }\\ \text{for }3< x\leq 10,\\ f\left ( x \right )=3x\\ \text{And,at }x=3\\ f\left ( x \right )=3^{2}=9\\ \therefore \text{at }x=3,f\left ( x \right )=9\\ \text{Therefore, for }0\leq x\leq 10,\text{the images of }f\left ( x \right )\text{ will be unique.}
Hence, the given relation will be a function.
Now,
According to the given relation g has been defined as:
g\left ( x \right )=\begin{Bmatrix} x^{2},0\leq x\leq 2\\ 3x,2\leq x\leq 10\end{Bmatrix}
We can see that,
\text{for }x=2\\ g\left ( x \right )=2^{2}=4\text{ and }g\left ( x \right )=3\times 2=6
The element 2 of the domain of g has two images 4 and 6.
Hence, the relation g is not a function.

2. If f\left ( x \right )=x^{2} , find
\frac{f\left ( 1.1 \right )-f\left ( 1 \right )}{1.1-1}[

Solution:
According to the given question,
f\left ( x \right )=x^{2}
Therefore,
\frac{f\left ( 1.1 \right )-f\left ( 1 \right )}{1.1-1}=\frac{\left ( 1.1 \right )^{2}-\left ( 1 \right )^{2}}{\left ( 1.1-1 \right )}=\frac{1.21-1}{0.1}=\frac{0.21}{0.1}=2.1

3. Find the domain of the function
f\left ( x \right )=\frac{x^{2}+2x+1}{x^{2}-8x+12}

Solution:
The given function is,
f\left ( x \right )=\frac{x^{2}+2x+1}{x^{2}-8x+12} f\left ( x \right )=\frac{x^{2}+2x+1}{x^{2}-8x+12}=\frac{x^{2}+2x+1}{\left ( x-6 \right )\left ( x-2 \right )}
We can clearly see that, the function f is true for all real numbers except for x=6\text{ and }x=2 as the denominator will become 0.
Hence, \text{Domain of f}=R-\left\{2,6 \right\}

4. Find the domain and the range of the real function f defined by f\left ( x \right )=\sqrt{\left ( x-1 \right )}.
Solution:
The given function is ,
f\left ( x \right )=\sqrt{\left ( x-1 \right )}
We can clearly see that, \sqrt{\left ( x-1 \right )} is defined for \left ( x-1 \right )\geq 0
Hence,
The function f\left ( x \right )=\sqrt{\left ( x-1 \right )} is defined for x\geq 1
Thus, the domain of f is the set of all the real numbers that are greater than or equal to 1.
\text{Domain of f}=[1,\infty)
Now we can see that,
As
x\geq 1\\ \left ( x-1 \right )\geq 0\\ \sqrt{\left ( x-1 \right )}\geq 0
Therefore, the range of f will be the set of all real numbers that are greater than or equal to 0.
\text{Range of f}=[0,\infty).

5. Find the domain and the range of the real function f defined by f\left ( x \right )=\left| x-1\right| .
Solution:
The given real function is,
f\left ( x \right )=\left| x-1\right|
It is clear that, the function \left| x-1\right| is defined for all the real numbers.
Therefore,
\text{Domain of f}=R
And, for x\epsilon R,\left| x-1\right| assuming all real numbers.
Hence, the range of f will be the set of all the non-negative real numbers.

6. Let f=\begin{Bmatrix}\left (x,\frac{x^{2}}{1+x^{2}} \right ):x\epsilon R\end{Bmatrix}
be a function from R into R. Determine the range of f.
Solution:
The given function is,
f=\begin{Bmatrix} \left ( x,\frac{x^{2}}{1+x^{2}} \right ):x\epsilon R\end{Bmatrix}

We’ll Substitute the values to determine the images, we have
=\begin{Bmatrix} \left ( 0,0 \right ),\left ( \pm 0.5,\frac{1}{5} \right ),\left ( \pm 1,\frac{1}{2} \right ),\left ( \pm 1.5,\frac{9}{13} \right ),\left ( \pm 2,\frac{4}{5} \right ),\left ( 3,\frac{9}{10} \right ),\left ( 4,\frac{16}{17} \right ),…..\end{Bmatrix}

The range of f will be the set of all second elements. It can be seen that all these elements are greater than or equal to 0 but will be less than 1.
[Since the denominator is greater than the numerator.]
And,
We also know that, for x ∈ R,
x^{2}\geq 0\\ \text{Hence,}\\ x^{2}+1\geq x^{2}\\ 1\geq x^{2}/\left ( x^{2}+1 \right )

Therefore,
\text{Range of f}=[0,1)

7. Let f, g: R → R be defined, respectively by f\left ( x \right )=x+1,g\left ( x \right )=2x-3 . Find f+g,f-g\text{ and }f/g.
Solution:
According to the question, the functions f, g: R → R is defined as

Hence,
\left ( f+g \right )\left ( x \right )=f\left ( x \right )+g\left ( x \right )=\left ( x+1 \right )+\left ( 2x-3 \right )=\left ( 3x-2 \right )\\ \text{Now,}\\ \left ( f+g \right )\left ( x \right )=\left ( 3x-2 \right )\\ \left ( f-g \right )\left ( x \right )=f\left ( x \right )-g\left ( x \right )=\left ( x+1 \right )-\left ( 2x-3 \right )=x+1-2x+3=-x+4\\ \text{Thus,}\\ \left ( f-g \right )\left ( x \right )=-x+4\\ f/g\left ( x \right )=f\left ( x \right )/g\left ( x \right ),g\left ( x \right )\neq 0,x\epsilon R\\ f/g\left ( x \right )=x+1/2x-3,2x-3\neq 0\\ \text{Hence,}\\ f/g\left ( x \right )=x+1/2x-3,x\neq 3/2

8. Let f=\left\{\left ( 1,1 \right ),\left ( 2,3 \right ),\left ( 0,-1 \right ),\left ( -1,-3 \right ) \right\} be a function from Z to Z defined by f\left ( x \right )=ax+b , for some integers a, b. Determine a, b.
Solution:
Given function,
f=\left\{\left ( 1,1 \right ),\left ( 2,3 \right ),\left ( 0,-1 \right ),\left ( -1,-3 \right ) \right\}
And the function f is defined as,
f\left ( x \right )=ax+b \text{For }\left ( 1,1 \right )\epsilon f\\ \text{We have, }f\left ( 1 \right )=1\\ \text{Then, }a\times 1+b=1\\ a+b=1….\text{(i)}\\ \text{For }\left ( 0,-1 \right )\epsilon f\\ f\left ( 0 \right )=-1\\ a\times 0+b=-1\\ b=-1
On substituting b=-1\text{ in (i)} , we get
a+(-1)=1\\ a=1+1=2
So,
a=2\\ b=-1

9. Let R be a relation from N to N defined by R=\left\{ \left ( a,b \right ):a,b\epsilon N\text{ and }a=b^{2}\right\} . Are the following true?
(i) (a, a) ∈ R, for all a ∈ N
(ii) (a, b) ∈ R, implies (b, a) ∈ R
(iii) (a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R.
Justify your answer in each case.
Solution:
The given relation is R=\left\{ \left ( a,b \right ):a,b\epsilon N\text{ and }a=b^{2}\right\}
(i) We can see that 2 ∈ N; however, 2\neq 2^{2}=4 .
Therefore, the statement “(a, a) ∈ R, for all a ∈ N” is false.
(ii) We can clearly see that that (9, 3) ∈ N because 9, 3 ∈ N and 9=3^{2} .
3=9^{2}=81;\text{hence, }\left ( 3,9 \right )\text{does not belong to natural number}
Therefore, the statement “(a, b) ∈ R, implies (b, a) ∈ R” is false.
(iii) We can clearly see that (16, 4) ∈ R, (4, 2) ∈ R because 16, 4, 2 ∈ N and 16=4^{2}\text{ and }4=2^{2} .
16\neq 2^{2}=4;\text{ therefore, }\left ( 16,2 \right )\text{ does not belong to natural number}
Therefore, the statement “(a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R” is false.

10. LetA=\left\{ 1,2,3,4\right\},B=\left\{ 1,5,9,11,15,16\right\}\text{ and }f=\left\{ \left ( 1,5 \right )\left ( 2,9 \right ),\left ( ,1 \right ),\left ( 4,5 \right ),\left ( 2,11 \right )\right\}. Are the following true?
(i) f is a relation from A to B (ii) f is a function from A to B.
Justify your answer in each case.
Solution:
According to the given question,
A=\left\{ 1,2,3,4\right\},B=\left\{ 1,5,9,11,15,16\right\}
Hence,
A\times B=\left\{ \left ( 1,1 \right ),\left ( 1,5 \right ),\left ( 1,9 \right ),\left ( 1,11 \right ),\left ( 1,15 \right ),\left ( 1,16 \right ),\left ( 2,1 \right ),\left ( 2,5 \right ),\left ( 2,9 \right ),\left ( 2,11 \right ),\left ( 2,15 \right ),\left ( 2,16 \right ),\left ( 3,1 \right ),\left ( 3,5 \right ),\left ( 3,9 \right ),\left ( 3,11 \right ),\left ( 3,15 \right ),\left ( 3,16 \right ),\left ( 4,1 \right ),\left ( 4,5 \right ),\left ( 4,9 \right ),\left ( 4,11 \right ),\left ( 4,15 \right )\left ( 4,16 \right )\right\}
Also,
f=\left\{ \left ( 1,5 \right ),\left ( 2,9 \right ),\left ( 3,1 \right )\left ( 4,5 \right ),\left ( 2,11 \right )\right\}
(i) A relation from a non-empty set A to a non-empty set B will be a subset of the Cartesian product A × B.
We can clearly see that f is a subset of A × B.
Therefore, f is a relation from A to B.
(ii)Since, the same first element, 2 corresponds to more than 1 image (9 and 11), relation f is not a function.
11. Let f be the subset of Z × Z defined by f=\left\{ \left ( ab,a+b \right ):a,b \epsilon Z\right\} . Is f a function from Z to Z: justify your answer.
Solution:
The given relation f is defined as:
f=\left\{ \left ( ab,a+b \right ):a,b \epsilon Z\right\}
We know that a relation f from a set A to B is a function if every element of set A has unique images in set B.
Since,
2,6,-1,-6\epsilon Z,\left ( 2\times 6,2+6 \right ),\left ( -2\times -6,-2+(-6) \right )\epsilon f\\ \text{i.e.,}\left ( 12,8 \right ),\left ( 12,-8 \right )\epsilon f
We can clearly see that, the same first element 12, corresponds to more than one image (8 and –8).
Hence, the relation f is not a function.

12. Let A=\left\{9,10,11,12,13\right\}\text{ and let }f:A\to N\text{ be defined by}f\left ( n \right )=\text{the highest prime factor of n.}. Find the range of f.
Solution:
According to the given question,
A=\left\{ 9,10,11,12,13\right\}\\ \text{Here, }f:A\to N\text{ be defined by}\\ f\left ( n \right )=\text{the highest prime factor of n.}
Therefore,
\text{Prime factor of 9}=3\\ \text{Prime factors of 10}=2,5\\ \text{Prime factor of 11}=11\\ \text{Prime factor of 12}=2,3\\ \text{Prime factor of 13}=13
Therefore, it will be expressed as
f\left ( 9 \right )=\text{The highest prime factor of 9}=3\\ f\left ( 10 \right )=\text{The highest prime factor of 10}=5\\ f\left ( 11 \right )=\text{The highest prime factor of 11}=11\\ f\left ( 12 \right )=\text{The highest prime factor of 12}=3\\ f\left ( 13 \right )=\text{The highest prime factor of 13}=13
The range of f will be the set of all f(n), where n ∈ A.
Therefore,
\text{Range of f}=\left\{3,5,11,13 \right\}