Profile
Settings
Refer your friends
Sign out
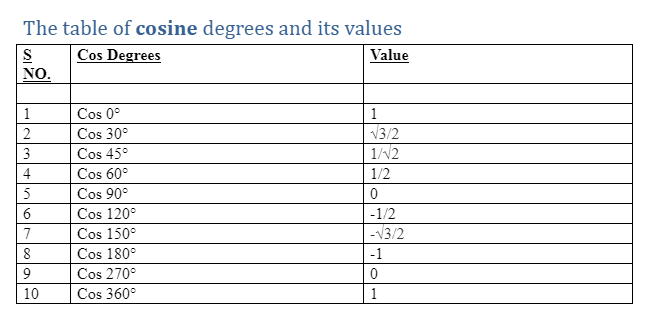
For a triangle, a cos function (or the cosine function) is a ratio of an adjacent side to the of the hypotenuse. The cosine function is the complement of sine (co + sine), and it is one of the three major trigonometric functions.
Cos is a ratio of the length of the adjacent sides to the length of the lengthiest side, the hypotenuse, in a right angled triangle. Assume, there is a triangle; BCD is there, with BC as = hypotenuse, BD as the base and as α, the angle between hypotenuse and base.
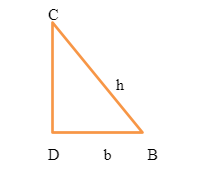
So, for the right triangle formed cos α= the adjacent side/hypotenuse.
So cos α will be equal to BD/BC.
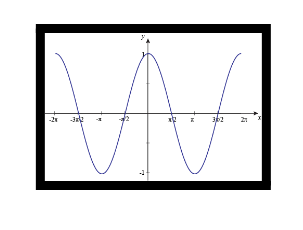
Graph of Cosine
The cosine graph, often known as the cos, is an up-down graph similar to the sine graph. The cos graph begins at 90 (or π/2). The cos graph shown below begins at 1 and falls to -1 before rising again.
Cos Identities
- cos² (x) + sin² (x) = 1.
- cos θ = 1/sec θ.
- cos (−θ) = cos (θ).
- arccos (cos (x)) = x + 2kπ [where k=integer].
- Cos (2x) = cos² (x) − sin² (x).
- cos (θ) = sin (π/2 − θ).
Cosine Rule
In trigonometry, the law of cosine or cosine rule is a relationship between sides of a triangle and angles. The cosine rule will be as follows if a triangle with side p, q, and r and angles P, Q, and R is taken.
Subsequently, according to cos law, the side “r” will be:
r² = p² + q² – 2pq cos (R)
Cosine Formulas
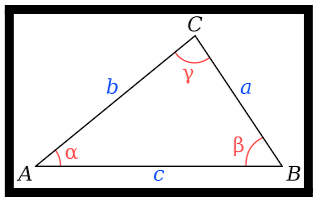
So, according to the formula of the cosines law, to take out the length of sides of triangle say in this triangle ABC, we can take as the following-
- c² = a² + b² – 2ab cos γ
- a² = c² + b² – 2cb cos α
- b² = a² + c² – 2ac cos β
And if we want to find the angles of △ABC, then the cosine rule will be used as;
- cos γ = [a² + b² – c²]/2ab
- cos α = [c² + b² – a²]/2cb
- cos β = [a² + c² – b²]/2ca
Where, the lengths of the sides of the triangle is a, and b and c
Solving the SSS Congruence
We know the lengths of all 3 sides of a triangle in SSS congruence, and we need to take out the measure of the unknown triangle. As a result, we may take the cosine rule to find the missing angle.
- To begin, we must find one angle using the cosine law, which is cos γ = [a² + b² – c²]/2ab
- Then, using the same law, cos α = [c² + b² – a²]/2cb, we can calculate the second angle
- Now you can easily find the third angle by using the triangle’s angle sum attribute, this means that the sum of a triangle’s three angles equals 180 degrees
Proof of Law of Cosine
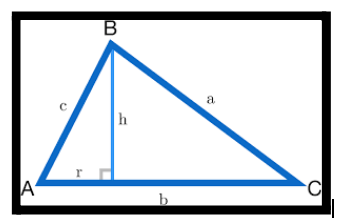
In the right triangle BAr, taking the cosine function definition-
cos A = Ar/c
or
Ar=c cos A
So, to subtract the equation above from side b, we get
rC = b − ccosA ……(1)
In the triangle BAr, according to the definition of sine
sin A = Br/c
or
Br = c sinA ……(2)
In the triangle CrB, so we use the Pythagoras theorem-
a² = Br² + rC²
Substituting for Br and rC from equations (1) and (2)
a² = (c sin A)² + (b-ccosA)²
So, in cross Multiplying we get:
a² = c² sin²A + b² – 2cbcosA + c² cos²A
So, in rearrange the equation above:
a² = c² sin²A + c² cos²A + b² – 2cb cosA
Taking out c² as a common factor, we get;
a² = c²(sin2A + cos²A) + b² – 2cb cosA
Now from the above equation, we know that,
sin²θ + cos²θ = 1
∴ a² = c² + b² – 2cb cosA
Therefore, the cosine law is proved.
Conclusion
When we determine the lengths of all the other two sides and the angle between them, we can apply the cosine law to find the third side of a triangle. Furthermore, It is not limited to right triangles and it can be applied to any sort of triangle in which an unknown side or angle must be found.
