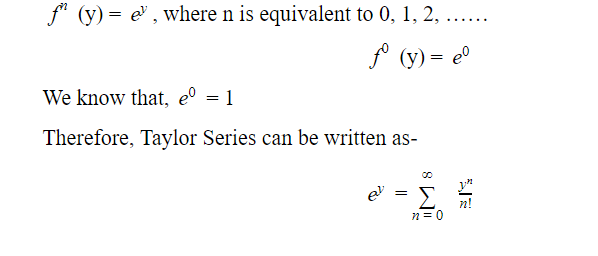Taylor Series (in one and two variables)

Let us start with a situation. Say, you are trying to solve a problem and end up getting a large and critical function. You think, you made some mistake and re-check all your steps. However, you could not find anything that needed correction or reconsideration. You sit with your hands on your head in utter hopelessness and frustration. You leave the room to get some fresh air- for instance, fresh ideas.  After a while, you come back to your room and tried solving the problem using the calculator. You put the critical function into your calculation. Finally, you get an answer which is not as complex as the function. You are happy. However, you start thinking about how the calculator did such a calculation in just a second? 

This kind of magic can be done by using a mathematical concept known as Taylor Series. Taylor Series method can help in making the calculation simpler when compared to the principal function. As we are growing up, the standard of mathematical concepts and methods is also growing. Every standard in school had a different type of math chapter. Each related to the concept of the previous standards. Math is evolving with us! And, we must always keep a track of all the different types of calculation methods- just so we can work with our mathematical problems easily. Taylor Series is one such calculation method. 

Let us understand briefly what is Taylor Series. 

Understanding Taylor Series

In Machine Learning, function approximation, Mathematics among others, Taylor Series can be a very useful concept. It is commonly used in numerical computations. In this method, the sum of a portion of the series can be estimated as an approximation of the whole series. This series is named after the famous mathematician Brook Taylor. As we know that Taylor series is a process of enlarging any function into a polynomial function that has a boundless number of terms in it. In the most basic sense, it is the method to enlarge a real function f(y) at a point y = b. This can be given by-

f (y) = f (b) + f’ (b) (y-b) + f” (b)2! (y – b)2 + …….. + fn (b)n! (y – b)n

Taylor series expansion is used only when y is equivalent to a certain point, which is not Zero. If the point is zero, I.e., y = 0, then it is known as the Maclaurin Series. It is named after Scottish Mathematician Colin Maclaurin. The above-mentioned Tylor Series formula is for a function with one variable. 

Taylor Series is basically about a point (say, b) till a certain order (say n), which is found using series- say, f {y, b, n}. Each of the succeeding terms will be higher than the previous term. Each of the terms in this series comes from the derivation of the function at a point. 

The above-given equation can also be said as the theorem of the Taylor Series. This equation can be written as-

n = 0 fn(b)n! (y – b)n

Now that we have understood what is Taylor Series, let us look at the Taylor Series formula for the trigonometric identity- Sin and Cos. 

Taylor Series formula of Sin 

The first step is differentiating Sin y till the nth term. Let us consider an easy point here. Let us find the Taylor Series for y = 0. 

f (y) = Sin y = 0

f’ (y) = Cos y =1

f” (y) = -Sin y =0

f”’ (y) = -Cos y = -1

.and this goes on till the nth term.

This will be given by- 

Sin y =  n = 0 fn(0)n! (y – 0)n

= n = 0 fn(0)n! yn

= y – y33! + y55! + ……..

Taylor Series formula of Cos 

The first step is differentiating Cos y till the nth term. Let us consider an easy point here. Let us find the Taylor Series for y = 0. 

f (y) = Cos y = 1

f’ (y) =  -Sin y = 0

f’’ (y) = -Cos y = -1

f’’’ (y) = Sin y = 0

.

.

and this goes on till the nth  term.

The Taylor series is given by-

Cos y =n = 0∞ fn(0)n! (y – 0)n

= 1 – y22! + y44! + ……..

Conclusion

As we are growing up, the standard of mathematical concepts and methods is also growing. Every standard in school had a different type of math chapter. Each related to the concept of the previous standards. Taylor Series method can help in making the calculation simpler when compared to the principal function. Taylor series is a process of enlarging any function into a polynomial function that has a boundless number of terms in it. Taylor Series is basically about a point (say, b) till a certain order (say n), which is found using series- say, f {y, b, n}. Each of the terms in this series comes from the derivation of the function at a point.