The standard deviation formula is used to calculate the standard deviation of a set of data. It is typically used in statistical analysis to determine the amount of variation from a given mean value. The formula for standard deviation is:
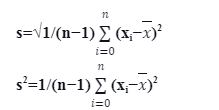
where x is the sample mean,
xi gives the data observations, and
n denotes the sample size.
Standard Deviation Formula:
The standard deviation formula is a mathematical function used to calculate the standard deviation in mechanical engineering. It is one of the essential formulas in mechanical engineering.
The standard deviation formula is applied to calculate how much variation there is between different measurements.
The standard deviation formula is a mathematical formula used in mechanical engineering and statistics to describe how much variation there is in a data set.
The standard deviation formula is used to calculate the average, the maximum, and the minimum values in a data set.
The formula for standard deviation is:
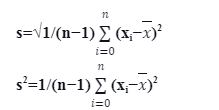
where x is the sample mean,
xi gives the data observations, and
n denotes the sample size.
Standard deviation:
Standard deviation measures the degree of variation or dispersion of a set of data values.
The mechanical engineering field has been seeing a lot of changes in recent years. New technologies are being introduced, new materials are being used, and new methods to make products. With these changes, engineers need to account for uncertainty and variability in their designs.
The standard deviation can measure the variation of data, such as the difference between two measurements. It is also used to compare different data samples, such as comparing two populations.
A standard deviation is a technique widely used statistical measure in engineering. It is used to measure the dispersion of a data set, and as a result, it can be used to assess how much variation there is within a given population.
The standard deviation is a measure of variation in a data set. It is calculated as a number between -1 and 1. A standard deviation is used to describe the variability of a data set. The standard deviation tells us how many times the data in our dataset will be different from the mean value, usually 0.
The term standard deviation refers to how much variation exists between different versions of content that various agencies or individuals create. In other words, it refers to how many times one version differs from another version of its content. To calculate this number, you need to know what your target audience wants and needs to purchase your product or service.
Mode deviation:
Standard deviation is the square root of the number of values that a function can take. For example, if we have a function with three parameters and four values in its range – 0 to 3 – then it has a standard deviation of 2 (2 x 2 = 4).
The mode deviation in mechanical engineering is an essential factor that plays a vital role in the performance of a machine. It refers to the difference between the natural frequency and damping ratio.
The mode deviation can be utilized to improve efficiency and performance by changing or designing machines to oscillate at their natural frequency or have a damping ratio close to it.
Mode and standard deviation:
The mode and standard deviation are two different measures of deviation. The mode refers to the value in a given data set that appears for the most number of times among other values in the set.
The mode deviation can be utilized to improve efficiency and performance by changing or designing machines to oscillate at their natural frequency or have a damping ratio close to it.
Standard deviation is one of the essential concepts in mechanical engineering. It is used to describe the variation of a variable in a process or system.
The standard deviation is calculated using the mode and the mean of a variable. The mode is the value that appears most often in a given data set. The mean is the average value of all values in a given data set.
Standard deviation measures how much data is dispersed from the mean value, while the mode is the most frequent value in a dataset.
Conclusion
Standard deviation measures how much an outcome varies from the average outcome for that type of measurement system or experiment. Standard deviation is calculated by subtracting the mean value from each set observation and dividing by its standard deviation. The standard deviation in mechanical Engineering is the amount by which a number deviates from its mean value. The mode of a distribution is the essential factor in understanding its shape and varies.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out




