The median is the middle value of a set of data. The median is the most common value in a distribution. It is a mathematical expression of the central number between two values.
The median is used to indicate the average value of a set of numbers.
Median is a summary of data, which can help compare two numbers. Medians can compare some data in a table and show an average value.
Median is also known as mean, mode, or mode line at work. The median is found by dividing each number by the number of digits in that set. For example, if there are 100 numbers and you split them all by 100, you get the median – which is 50%.
The median is also known as the middle number, and it’s used in mathematics and statistics. The median is also used to measure the centre of a circle or any other polygon shape.
When it comes to mechanical engineering, the median (the middle value) is a valuable measure of the average distance between two values in a set.
The median in mechanical engineering is one of the most important numbers. It is used as a basis for calculating the probability of different outcomes.
The median is a valuable statistic to measure the middle of a set of numbers. It is also used to find which number is the midpoint between two numbers.
Jensen’s inequality is a mathematical property of the median in a data set. Jensen’s inequality states that if you have n observations, then the median is always equal to the mean of those n observations.
How come it is equal to the mean? It’s simple: If you have an observation x1 and another observation, then there are two possibilities: or. If they are both less than 10, we can say that their sum is ten or greater than 10. In other words, if you are looking at two numbers with a total value of 11 and one number with a total value of 12, then for them to be equal to.
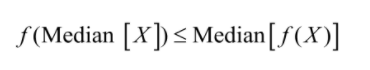
The median can solve problems such as finding the average value or finding which line intersects the others at a given point.
Formula:
A median is a simple number used to measure distances between various numbers or quantities. The median of two numbers or quantities is found by subtracting their difference from the total. To find the median of three numbers or quantities, you multiply their difference by two and then add their sum.
This method works because when you multiply two numbers, they cancel each other out, leaving only one number left. For example, if we multiply 200 by two and then add it to 900, we get 300 as our result because 300 + 200 = 900, which is also close to 300, so we can use this method to find the median of these three numbers.
The median of two numbers is found by dividing them both by two (or multiplying them both by 2)
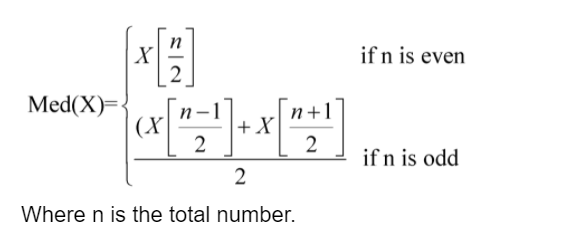
Finding the median:
There are many ways to find the median in a data set, but the most popular form of doing it is by using a histogram. A histogram shows the distribution of numbers, and each number has its position in the histogram. The higher up on this histogram, the more values fall into that particular range of numbers (the range). The lower down on this histogram means fewer values for that specific range (the minimum).
The median, also called the middle point, is one of the most commonly used numerical values for measuring centrality in any setting. This value can be used in many ways: to compare two sets, to find the average or mean value among several sets, etc.
It can also be calculated using other methods such as arithmetic mean or geometric mean. However, it is essential to note that these methods are not always valid because they do not consider any context information, such as the size or shape of any set. For example, there may be more than one way to measure centrality, and only one could be used when calculating.
Meaning of Median:
Median is defined as “the quantity of an item that falls between two numbers”. The two numbers are called the “median” and “min”. To find the median value for an item in a collection of items
divide all values below it by all values above it, then sum all remaining values from 1 to the number of items in the group.
The median value (or mean) is the value that is halfway between the two extremes. The median is a measure of central tendency. It is used to define the middle of a set of data points.
Conclusion:
The median is the point in a distribution where half of the values are above and half are below. The concept is useful when we want to determine how many people are in a group or how many people are in a group. The median, also called the middle point, is one of the most commonly used numerical values for measuring centrality in any setting. This value can be used in many ways: to compare two sets, to find the average or mean value among several sets, etc. Jensen’s inequality is essential in the median.
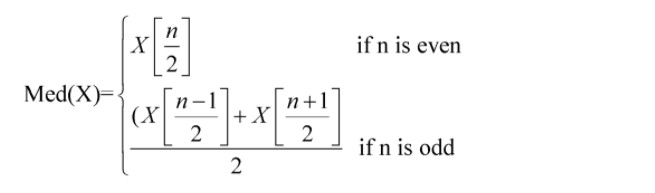
Where n is the total number.
The formula for Jensen’s inequality is 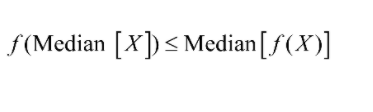
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






