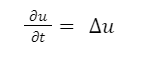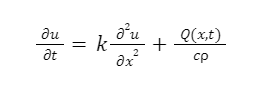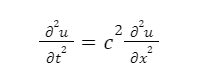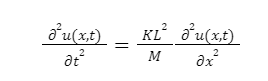Laplace, Heat and Wave Equation

Laplace, Heat, and Wave equations are known as the three fundamental equations of Physics. A partial differential equation includes an equation that consists of several unknown variables as functions, relating to their partial derivatives. A partial differential equation is one of the most crucial equations to understand the various aspects of physical and mathematical concepts including heat, sound, waves, etc. These equations play a vital role in performing various physical calculations that are helpful in electric circuit theory to solve the switching transient phenomena, determining the harmonic vibration in a beam, weather forecasting, and solving problems related to fluid mechanics.

LAPLACE EQUATION:

Laplace’s Equation was postulated by Perry-Simon Laplace, a French mathematician, and astronomer. Laplace’s equation is used to determine the sum of the second-order partial derivatives of any unknown function, concerning Cartesian coordinates. Mathematically, it is expressed as:

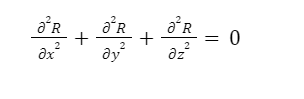
In Laplace’s equation, the unknown variable is considered to be a harmonic function that helps in solving several problems related to hydrodynamics, gravitational potentials, heat, etc.

HEAT EQUATION:

The heat equation is a partial differential equation that consists of a function that is called caloric function. Basic vision was postulated by Joseph Fourier in 1822, to determine the heat behavior. Based on the Laplacian response, a heat equation is expressed as:

Here, keeping the time as a variable, u is considered to be the solution of the heat equation. denotes of positive coefficient which is also termed as thermal diffusivity of the medium. The mathematical expression of this equation is:

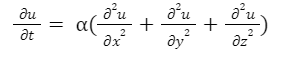
HEAT EQUATION FORMULA:

Several terms used in the heat equation formula are:

u(x,t)= Temperature at any point x and any time T.

c(x)= Specific Heat.

(x)= Mass density.

(x,t)= Heat Flux.

Q(x,t)= Heat Energy generated per unit volume per unit time.

Based on these mathematical terms, the heat equation formula is expressed as:

As the formula was compelled with several unknown factors to get rid of them, Fourier’s Law came into consideration. Applying the Fourier’s law and simplifying the heat equation formula, it is expressed as:

WAVE EQUATION:

A wave is defined as any disturbance cost in the medium during the transfer of energy without the movement of the particles. A wave is responsible for the variation in the pressure or any deformation caused and even the frequency. To determine the behavior of the waves, a Wave equation is considered. A Wave equation is a second-order partial differential equation that determines the wave behavior in the form of these scalar functions or vector functions, with multiple unknown variables. The mathematical expression of the Wave equation in one space dimension is:

Here, the Wave equation is determined in one space direction x under the variable of time t.

WAVE EQUATION FORMULA:

A Wave equation formula is derived with the help of Hooke’s law as determined in the theory of elasticity. Considering a massless spring of length L=Nh, interconnected with an array of weights of mass M=Nm placed at a certain distance from each other. The equation of motion for such weights at a distance x+h is expressed as:

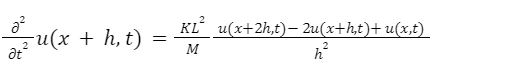
Here, k denotes the spring constant. Whereas, K=k/N

Now limiting the equation as N→∞, h→0 will give out the result:

Though, there is a provision of the Wave equation calculator that helps in determining the solution of any wave equation easily by inputting the value of u and ut. The Wave equation calculator provides an accurate solution along with the graphical representation of the waves.

CONCLUSION:

Laplace, Heat, and Wave equations are the 3 fundamental partial differential equations that play a great role in the scientific field. Laplace equation is used in solving problems related to electric circuits. Power generators, voltage stabilizers, etc. The Heat equation plays a vital role in weather forecasting, geophysics as well as solving problems related to fluid mechanics. The Wave equation is determined to study the behavior of the wave in a medium. To understand the concept of Laplace, heat, and wave equation better, it is suggested to go through the Hooke’s Law, Laplace transform and methods of solving the partial differential equation as well as laws of thermodynamics.