Fourier, Taylor and MacLaurin Series

Fourier, Taylor, and MacLaurin Series are popular concepts used in various fields like telecommunications, computer science, chemistry, physics, calculus, and other mathematics solutions. 

All the concepts revolve around polynomials and derivatives. In this article, we will dive deep and understand the core meaning and usage of these concepts.

Meaning of Fourier Series:

The Fourier series in very simple words helps in expanding a periodic function f(x) in terms of an infinite sum of sines and cosines. The orthogonality relationships between sine and cosine are used. 

Jean-Baptiste Joseph Fourier (1768–1830) is the person who founded the Fourier series. The series can only be used if the functions are periodic in nature.

This concept is primarily used while studying engineering since most of the concepts in engineering are periodic. 

The study of the Fourier series is referred to as harmonic analysis. The concept helps in breaking down complex arbitrary periodic functions into simple terms.

Further, these simple terms can be solved individually. Once they are solved the terms can be combined to find a solution to the original problem.  

Formula of Fourier Series:

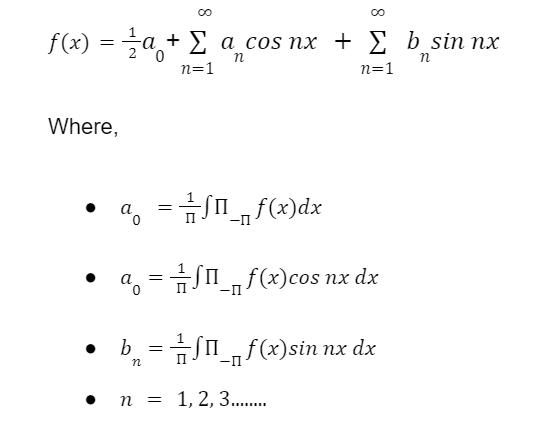
Advantages of Fourier Series:

• It can help in representing a discontinuous function.
• Using Fourier the series you can easily represent a function or signal in the form of an infinite sum of sine wave components. 

Meaning of Taylor Series:

The main function of the Taylor series is to represent a function as an infinite sum of terms. This further helps in calculating the values of its derivatives at a single point.

Now, you may ask why we should even use an infinite sum of terms? Great question! If we have more terms in our approximated function then the chances of getting an approximation to the real value are much higher.

This concept was introduced by Brook Taylor in 1715.

The theory behind the Taylor series suggests that if we put up a point on the coordinate plane (x- and y-axes) then we can find out what the function will look like around that point.

Formula of Taylor Series:

Advantages of Taylor Series:

• The Taylor series is extremely helpful when you are solving derivatives.
• You can easily convert any complex sum into an easy one.
• If you want theoretical error bounds from the sum then you can use the Taylor series.

Meaning of MacLaurin Series:

The MacLaurin series is a special kind of Taylor polynomial that uses zero as the single point.

This series is mainly used in sine function. We all know that the sine function makes it difficult to compute the output values for the function at arbitrary input values. Although this process can be simplified if we use sin(x) when x=0.

So, the MacLaurin series formula uses zero as the single point.

To calculate the precise approximations of sin(x) we can take the help of this series to use one of the derivatives at zero. This series can easily estimate the antiderivative of a complex sum.

At its core, the MacLaurin series is nothing but the Taylor series when the function is at zero. Both the Taylor and MacLaurin series helps us to turn a difficult sum into something easy to solve.

Formula of MacLaurin Series:

The MacLaurin Series formula is similar to the Taylor Series. Although in the MacLaurin series the a = 0

Advantages of MacLaurin Series:

• Solve any difficult derivative problem with ease.
• Find the antiderivative of a complex sum.
• You can easily integrate and differentiate the functions in order to find representations of other functions.

Conclusion:

So, to conclude, the Fourier series is focused on expanding a periodic function in an infinite sum of sines and cosines. 

On the other hand Taylor series represents a function as an infinite sum of terms and the MacLaurin series uses zero as the single point. 

With the help of these series, we can easily simplify a complex sum into simple terms and solve the problem with ease.

All these concepts are very important and without them solving polynomials, derivatives would be a tough job