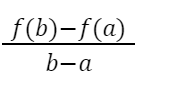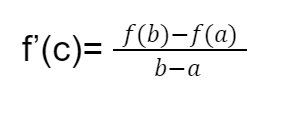In the 14th Century, a mathematician named Parameshwara, from Kerala proposed the first form of the Mean Value Theorem.

According to the Mean Value Theorem, if a curve is passing through any two points, then there is one point on the curve on which if we draw a tangent, the tangent would be parallel to the secant line passing through the two-point.

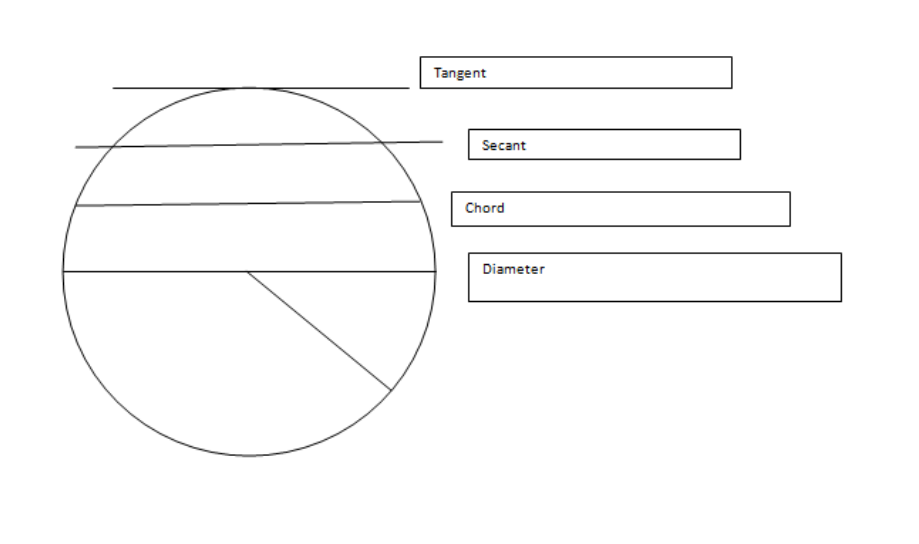
WHAT IS THE MEAN VALUE THEOREM?

Let’s suppose there is a curve f(x) that is passing through two given points (a, f(a)) and (b, f(b)).

The Mean Value Theorem states that there is at least one point on the curve (c, f(c)) such that the tangent to it is parallel to the secant through the point (a, f(a)) and (b, f(b)).

The function f(x) is defined f(x): [a, b] R such that f(x) is continuous and differentiable across the interval [a, b].

• f(x) is continuous across the interval [a,b].

• The function is differentiable across the interval (a, b).
• There will be a point (let’s suppose c) c between the interval (a,b) such that the slope of this point can be calculated as:

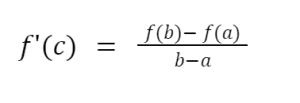
MEAN VALUE THEOREM FORMULA

In the above figure, to find a slope of the tangent on the curve, we could use the formula:

Slope (let’s suppose ‘m’) = Y’ – Y÷X’ – X

If we put value Y’ = f(b), Y = f(a) and X’ = b, X= a in the above equation, we could arrive at the Mean Value Theorem formula:

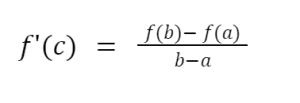
LAGRANGE MEAN VALUE THEOREM.

Lagrange Mean Value Theorem is another name of the Mean Value Theorem. The Special Case of the Lagrange Mean Value Theorem is known as the Rolle Theorem.

Suppose for example in the above graphical representation, f(a) = f(b), then according to the said formula, f’(c)=0. Assume a and b as real numbers.

This theorem is now called Rolle’s Theorem which was put forward by the famous mathematician Michael Rolle in the 17th Century.

PROOF OF LAGRANGE MEAN VALUE THEOREM.

If a function f(x) is continuous over the closed interval [a, b] and differentiable over an open interval (a, b) then there will be at least one point on the curve (let’s name it c) c, such that slope of the tangent over it would be equal to the slope of the secant line passing through the point (a, f(a)) and (b, f(b)).

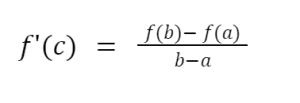
PROOF:

Let the curve be f(x) and the secant line be s(x). The secant line s(x) is passing through the point (a, f(a)) and (b, f(b)).

The slope of the secant line:

Slope, m =

The equation of the secant line:

Y- Y’ = m (X-X’)

If we put values of Y’ = f(a) and X’= a in the above equation,

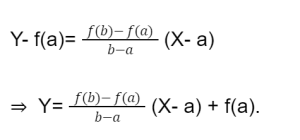
The equation of secant line s(x) = Y, putting values in the above equation.

Lets g(x) be another function such that,

g(x) = f(x) – s(x) ——— (2)

If we put equation (2) in equation (1), we have,

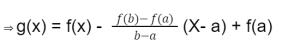
Let us consider that the function g(x) is continuous between [a, b] and differentiable between (a, b), then according to Rolle’s theorem, there would be at least one point (let’s take it as c) between a and b such that g’ (c) = 0.

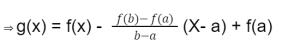
The point c between the interval (a, b), such that g’(x)= g’ (c ) = 0.

EXAMPLE ON LAGRANGE MEAN VALUE THEOREM

Example– Find out if the function x² + 4x -8 satisfies the Lagrange Mean Value Theorem between the interval (-3, 3).

SOLUTION:

f (x) = x² + 4x -8 at interval (-3, 3)

f'(x) = 2x + 4 …. (1)

f(-3) = 9 + 4*(-3) – 8 =  9 -12 – 8 = -11

f(3) = 9 + 4× 3 – 8= 9 + 12 – 8= 13.

f'(x)= f(3)- f(-3)/3- (-3)

f'(x)= 13- (-11)/6= 4 ……(2)

f'(c) = 4

If we equate equation (1) and equation (2), we have,

2x + 4 = 4

If we put x=c in the above equation,

2c + 4 = 4

c= 0

Here, c = 0 lies in the interval (-3, 3).

CONCLUSION

Here since c=0 lies in the interval (-3, 3), therefore the given function

x² + x -8 satisfies the Lagrange Mean Value Theorem.