The second-order partial differential equation which is commonly used in physics as its solution R also known as harmonic functions takes place in problems related to electric, magnetic and gravitational potentials of state temperatures as well as of hydrodynamics is called Laplace’s equation. The French mathematician and astronomer Pierre-Simon Laplace discovered Laplace’s equation.
According to Laplace’s equation the total of second-order partial derivatives of R, the unknown function, as per the Cartesian coordinates, is equal to zero.
Laplace’s equation can be depicted as:
![]() Some pivotal points to note about Laplace’s equation are:
Some pivotal points to note about Laplace’s equation are:
Uyy + Uxx = Urr + (1/r)Ur + (1/r2)Uθθ = Zero
For the heat equation, the solution U(x,y,t) is equal to U(r, θ, t), that is,
Ut is equal to K(Uxx +Uyy) which is equal to K[urr +(1/r)ur + (1/r2)uθθ] where,
K > zero: diffusivity
On the other hand, for the wave equation, one can see,
Utt is equal to c2(uxx +uyy) is equal to c2[Urr + (1/r)Ur +(1/r2) Uθθ] where,
C > zero:wave velocity
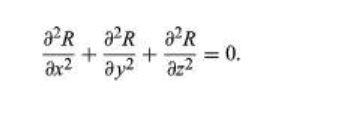 Some pivotal points to note about Laplace’s equation are:
Some pivotal points to note about Laplace’s equation are:
- The equation does not have a dependence on time rather it has a dependence on the spatial variables such as x and y.
- Laplace’s equation can also be described as a steady-state equation such that it has steady-state temperature distribution, stress distribution and potential distribution.
Laplace’s equation in polar coordinates
After leading to the derivation of Laplace’s equation in polar coordinates, it can be convenient in representing the heat and wave equation in polar coordinates. Laplace’s equation in polar coordinates can be described as:Uyy + Uxx = Urr + (1/r)Ur + (1/r2)Uθθ = Zero
For the heat equation, the solution U(x,y,t) is equal to U(r, θ, t), that is,
Ut is equal to K(Uxx +Uyy) which is equal to K[urr +(1/r)ur + (1/r2)uθθ] where,
K > zero: diffusivity
On the other hand, for the wave equation, one can see,
Utt is equal to c2(uxx +uyy) is equal to c2[Urr + (1/r)Ur +(1/r2) Uθθ] where,
C > zero:wave velocity
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out




