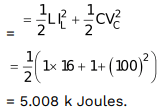Network Analysis

Q.1. The value of ‘V’ from the given below circuits is _______V.

Sol. –10 V

By redrawing the given circuit

Current flowing through 30 Ω is zero.

So, circuit becomes

Current flowing through 20 Ω resistor is

= 0.5 Amp

V = –0.5 × 20 = –10V

Q.2. For what value of R1 maximum power dissipated in R2.

(a) R1 = ∞

(b) R1 = 0

(c)

(d) R1 = R3

Sol. Correct answer (a)

For maximum power dissipated in R2is

Pmax = I2 R2

Where I is the current flowing through R2.

Here current through R2 must be maximum for maximum power dissipation in R2.

For current through R2 maximum, the value of R1 should be maximum because R1 and R2 are connected in parallel.

So, by looking option if R1 = ∞

Total current will flow through R2, hence maximum power dissipation.

Q.3. Find equivalent resistance across terminal ab

(a) 26.5 Ω

(b) 30 Ω

(c) 28.28 Ω

(d) None of these

Sol. Correct answer (c)

Considering given circuit as a cascade connection of T-network.

Req = 20 + (20 + Req) || (10)

⇒ Req (30 + Req) = 600 + 20 Req + 200 + 10 Req

Q. 4. For what value of ‘a’ maximum power transformer to 20 Ω and also maximum value of power in watts respectively.

(a) 5, 2

(b) 10, 2

(c) 2, 5

(d) 2, 10

Sol. Correct answer (c)

Using Thevenin’s theorem the given circuit can be reduced as

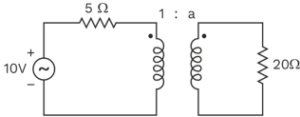
For maximum power transferred to 20 Ω load.

RL = Rth

a = 2

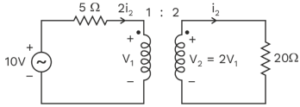
Writing KVL

–10 + 5 × 2 i2 + V1 = 0

⇒ V1 + 10 i2 = 10 ……….. (1) Writing KVL

–2V1 + 20 i2 = 0 ……….. (2) Solving equation (1) and (2) 40 i2 = 20

i2 = 0.5 A

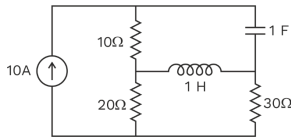
Q. 5. Total energy stored on network at steady state is-

(a) 5 kJ

(b) 7 kJ

(c) 8 kJ

(d) 10 kJ

Sol. Correct answer (a)

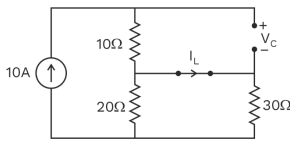
At steady state inductor behaves as short circuit and capacitor behaves as open circuits.

By drawing the circuit at steady state

VC = 10 × 10 = 100 V

Total energy stored in the network is