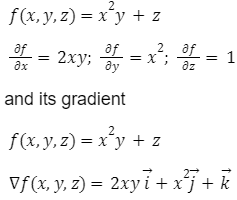The Gradient of a Scalar Field

A scalar field’s gradient is a vector field whose magnitude represents the rate of change and which points in the general direction of the scalar field’s greatest rate of increase. The components of the vector, if it is resolved, show how quickly the scalar field is changing in relation to each directional component. Only if the provided vector is differential can we convert the vector field into a scalar field. For the gradient phenomenon to apply, the provided vector must be differential. Any scalar field’s gradient reveals the rate and direction of change it undergoes in space.

Scalar field

1. Scalar field difficulties are a type of physical phenomena that underlies a number of engineering problems. In other words, when a scalar quantity changes along a continuum. Typically, we must determine the scalar quantity’s value, gradient, and occasionally integral over the problem domain. Scalar fields are frequently used in such domains as electrical conduction, heat transfer, irrotational fluid flow, magneto statics, seepage in porous media, torsion stress analysis, and others. The well-known Laplace and Poisson differential equations frequently govern these issues. It can be challenging to find an analytical solution for these equations in two- and three-dimensional field problems, particularly when there are intricate boundary conditions and irregularly shaped regions.

2. A very efficient and flexible method of solving this class of problems has been the finite element formulation using Galerkin or variational approaches. The previous challenges brought on by complex boundary conditions and uneven geometry are essentially gone. The formulation of the steady-state heat conduction problem’s solution will serve as an introduction to the subsequent development. The method is broad, though, and by redefining the physical parameters involved, the formulation can be used to solve a variety of Poisson equation-related issues.

3. A scalar field connected to the surface S can be described by the function f. For instance, S could could be a combustion engine component’s surface and f might be the surface temperature as a function of position. Alternately, S could be the earth’s surface and one of the following values recorded at various S locations: altitude above sea level, temperature, magnetic field intensity, etc. Another illustration is the goal of determining the pressure at any given position on an aeroplane wing given values of f measured on S, such as discrete pressures on the wing. Another instance that is relevant to CAGD is where f denotes a scalar field that represents a feature of S’s visual appeal, like the Gaussian curvature.

The gradient of a scalar field

A scalar function’s (or field’s) gradient is a vector-valued function that is directed in the direction of the function’s fastest rise and has a magnitude equal to that increase’s speed. It is represented by the symbol (called nabla, for a Phoenician harp in greek). As a result, the gradient is a directional derivative. Every point in the space is given a number (a scalar value) via a scalar function.

Gradient in Cartesian coordinates:

Here ∂ symbol represent the partial derivative of function f with respect to corresponding variable, When a scalar function depends on more than one variable, the partial derivative of that function with respect to that variable is calculated while the other variables are kept constant.i,j and k are unit vectors for directions x,y and z axiz.

Example of partial derivatives of a scalar function:

Vector operator

Similar to dynamic arrays, vectors can dynamically resize when an element is added or removed, with the container managing their storage on their behalf.

In vector calculus, a vector operator is a differential operator. The gradient, divergence, and curl are examples of vector operators whose definitions are expressed in terms of del:

 grad≡∇

 div≡∇.

 curl≡∇ ×

The Laplacian is 

∇²≡div grad ≡∇.∇

In order to obtain a result, vector operators must always come exactly before the scalar or vector field on which they operate. E.g.

∇f

The Laplacian is an example of a compound vector operator, which is created when a vector operator operates on another vector operator.

Conclusion

The greatest rate of change for a scalar field with respect to position is represented by its gradient, which is always parallel to the field surface at that point. The gradient of a scalar field is also known as the directional derivative of a scalar field since it is always directed along the normal direction. Any scalar field’s gradient reveals the rate and direction of change it undergoes in space. The formulation of the steady-state heat conduction problem’s solution will serve as an introduction to the subsequent development. Scalar fields are frequently used in such domains as electrical conduction, heat transfer, irrotational fluid flow, magneto statics, seepage in porous media, torsion stress analysis, and others.