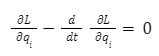Lagrangian and Hamiltonian Formalism and Equations of Motion

Two major formulations of classical mechanics—Lagrangian mechanics and Hamiltonian mechanics—were created as the theory evolved into more complex and in-depth forms of advanced mechanics that expressed the rules of physics in a more fundamental manner. The Euler-Lagrange equation, which has to do with how a quantity called action describes the trajectory (path in space) that a particle or a system will travel, is used in Lagrangian mechanics to derive the equations of motion.

Lagrangian and Hamiltonian Formalism 

We are aware that a mechanics problem’s tractability can be greatly affected by the choice of variables (coordinates). For instance, a lever can be modelled as either a “lever arm” with only one position coordinate (the angle, ) and the property of “rigidity,” or as a nearly infinite number of atoms. Although we are prone to think that the second version is superior to the first, Hamilton understood that occasionally even more coordinates might provide more information. He acknowledged that it is not always desirable to have the simplest, most economical description. Particularly, Hamilton increased the number of coordinates in any mechanics issue by two. This wasn’t just a simple doubling of dimensions.

The differences between Hamilton’s mechanics and Lagrangian mechanics will be clarified through a brief allegory, which will also explain why we bother. Imagine that we are avid golfers who wish to get better at the game. On Saturday, we are at the 18th hole’s tee, with the appropriate golf club in hand. We also have a large supply of similar golf balls. We start hitting 100 balls in the direction of the 18th flag. We count the number of balls we find on the putting green as we make our way there, exhausted. The following day (Sunday), we drive 100 balls once more, but as we approach hole 18, it begins to rain, so we decide to head for the clubhouse instead, where tea and scones are waiting for us. Even while it may appear that there are many differences between the two formulations of mechanics, they are really just two sides of the same classical mechanics coin that use distinct perspectives to describe the same events. Both of these formulations, though, have advantages of their own. The Lagrangian and Hamiltonian formulations are also analogous to Newtonian mechanics in the framework of classical mechanics.

Lagrangian Equation of Motion

The Euler-Lagrange equation, which deals with how a quantity called action specifies the trajectory (path in space) that a particle or a system will travel, is how the equations of motion in Lagrangian mechanics are obtained. Anyhow, the Euler-Lagrange equation naturally incorporates second derivatives because it is a second order differential equation. The complete equation is shown below:

I’ll simply quickly go over the specifics of this equation because we’ll need them later on for more in-depth discussion. Simply put, the q and q’  represent location and its time derivative (i.e. velocity, denoted by putting a dot above it). Although the generalised location and velocity coordinates are more exact, this isn’t really significant for our needs here.

Here, the L stands for the system’s Lagrangian, which is a function that essentially characterises motion as the difference between kinetic and potential energy.

But how exactly is this second order differential in the Euler-Lagrange equation?

If you remember that q, the velocity is simply the time derivative of the position, you will see that the equation contains a second order derivative with regard to time. The velocity term is then time differentiated once more as a result of the other time derivative term (becoming acceleration).

Conclusion

One of the most effective methods for studying dynamic systems is through the use of the Lagrangian and Hamiltonian formalisms. The fact that Lagrangian mechanics primarily deals with position and velocity in Lagrangian mechanics and Hamiltonian mechanics uses both to describe motion is one of the primary distinctions that becomes clearly significant in fields like quantum mechanics. While there aren’t really any substantial distinctions between the two in classical mechanics, it becomes clear why momentum would be preferable to velocity once you start studying relativity and quantum mechanics.