Rules of Algebra

The fundamentals of algebra teach students how to apply algebraic concepts to elementary mathematical operations such as addition, subtraction, multiplication, and division using both constants and variables. For example, x + 10 = 0. Equations, a fundamental concept in algebra, are presented here as an example of this. The algebraic equation can be conceptualised as a scale, with the “weights” being represented by numbers or constants, and the scale is balanced.

In algebra, letters of the alphabet are substituted for numbers in order to solve mathematical problems. Algebra is a subfield of mathematics. These alphabetic characters are also referred to as variables. The values, such as numbers, that are known to be present in the expression being evaluated are referred to as constants. The concept of algebra at the potential level will be taught to students even though they are in higher-level classes. However, when we talk about its fundamentals, it encompasses the general algebraic expressions, formulas, and identities that are used to solve a wide variety of mathematical issues.

Algebra Basics

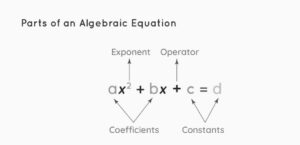
In order for us to understand the fundamentals of algebra, it is necessary for us to be familiar with the terminology that is associated with it. An expression known as an algebraic equation contains a variable, an operator, an exponent, a coefficient, and a constant, as well as the symbol for equal to connect all of these components together. Let us take an equation, ax² + bx + c = d. When doing algebra, you begin by writing the term that has the highest exponent, and then you write the subsequent terms with reducing powers.

There are four terms in the equation ax² + bx + c = d, which can be seen above. An algebraic equation may contain different terms that are the same or different from one another. When solving an equation, like terms are terms that have the same variables and exponents. On the other hand, terms in an equation that are dissimilar to one another constitute distinct variables and exponents.

Algebra Rules

There are five fundamental rules that makeup algebra. They are as follows:

•Commutative Rule of Addition

•Commutative Rule of Multiplication

•Associative Rule of Addition 

•Associative Rule of Multiplication

•Distributive Rule of Multiplication

1)Commutative Rule of Addition

The commutative rule of addition is a fundamental concept in algebra. According to this rule, the order in which two terms are added together does not affect the final result. (a+ b) =(b+ a) is the equation that describes the same thing. For example, (x³ + 2x) = (2x + x³)

2)Commutative Rule of Multiplication

According to the commutative rule of multiplication, when multiplying two terms, it does not make a difference which orders the multiplication is performed in (a.b) = (b.a) is the equation that describes the same thing mathematically. For example, (x⁴ – 2x) × 3x = 3x × (x⁴ – 2x).

LHS = (x⁴ – 2x) × 3x = (3x⁵ – 6x²)

RHS = 3x × (x⁴ – 2x) = (3x⁵ – 6x²)

Since the left-hand side (LHS) equals the right-hand side (RHS), this demonstrates that the two sets of values are comparable.

3)Associative Rule of Addition

According to the associative rule of addition in algebra, when three or more terms are added together, it does not matter what order the additions are performed in. The corresponding equation is written as follows: a + (b + c) = (a + b) + c. For example, x⁵ + (3x² + 2) = (x⁵ + 3x²) + 2

4)Multiplication according to the Associative Rule

In a similar vein, the associative rule of multiplication states that it does not make a difference in which order the terms are multiplied when there are three or more terms being multiplied together. The corresponding equation is written as follows: a plus (b plus c) equals (a plus b) plus c. For example, x³ × (2x⁴ × x) = (x³ × 2x⁴) × x.

Distributive Rule of Multiplication

According to the distributive rule of multiplication, the answer that we get when we multiply a number by the addition of two other numbers should be the same as the sum of the products those numbers have when they are multiplied by the number on their own. This demonstrates the prevalence of multiplication in comparison to addition. The corresponding equation reads as follows: a x (b + c) = (a.b) +(a .c). For example, x²× (2x + 1) = (x² × 2x) + (x²× 1).

Conclusion

One of the many subfields that fall under the umbrella of mathematics is called algebra. Algebra, in a broad sense, refers to the study of mathematical symbols as well as the rules that govern how these symbols can be manipulated within formulas. In algebra, letters of the alphabet are substituted for numbers in order to solve mathematical problems. Algebra is a subfield of mathematics. These alphabetic characters are also referred to as variables. The values, such as numbers, that are known to be present in the expression being evaluated are referred to as constants. There are five fundamental rules that makeup algebra. They are as follows: Commutative Rule of Addition, Commutative Rule of Multiplication, Associative Rule of Addition, Associative Rule of Multiplication, Distributive Rule of Multiplication.