Primitive roots are considered to be the smallest positive power that can correlate two integers, which are comparatively prime with each other. The Euler-Fermat formula determines the evaluation of primitive roots. The outcome of the primitive roots can be a quadratic residue or a quadratic non-residue. A quadratic equation is determined as a complex equation where the polynomial has the power of degree two at the most. Otherwise, it will be considered as a linear equation. The simplification of the primitive roots and the quadratic equation correlates with the evaluation of square roots. The Sridharacharya formula is used for simplifying the quadratic equation.

ROOTS OF QUADRATIC EQUATION:

A quadratic equation is determined to be a complex equation of numbers with a polynomial that has the degree two. A Quadratic Equation is represented as:

ax2+bx+c=0

In this formula, if a=0, then the equation no longer remains a quadratic equation because the highest value x2 is eliminated. Hence, it comes in the form of a linear equation. In a quadratic equation, x is an unknown number, whereas a,b, and c are the real numbers. Evaluation of the quadratic Equation is done by the method of Sridharacharya formula, which is expressed as:

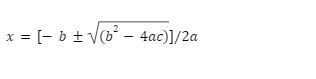
SQUARE ROOTS:

The square root of a number is a number whose multiplication by itself will give the original number. However, a square root can be determined as an inverse of squaring a number. 

PROPERTIES OF SQUARE ROOTS:

NATURE OF ROOTS OF QUADRATIC EQUATION:

There are several roots of the quadratic equation. These natures of roots are dependent upon the discriminant of the quadratic equation. The discriminant of a quadratic equation is evaluated by (b2-4ac) postulated by the Shridharacharya formula. Based on the discriminant values, there are five natures of roots. They are:

  • Real roots: An equation is the real root of a quadratic Equation; if the value is a real number, that condition can be achieved only if the discriminant of that quadratic equation is greater than zero, i.e., (b2-4ac) > 0.
  • Imaginary roots: An equation is said to be the imaginary roots of quadratic equations, only if the discriminant of the equation is less than zero, i.e., b2-4ac < 0.
  • Rational quadratic Equation: A root of a quadratic equation is rational if the quadratic equation’s discriminant is a perfect square.
  • Irrational quadratic Equation: In contrast to the rational quadratic equation, the irrational quadratic equation is defined as a quadratic Equation whose discriminant is not a perfect square.
  • Equal roots: A quadratic equation is said to be the equal nature of roots; only if the discrimination of the quadratic equation is equal to zero (b2-4ac=0) then it is termed as a real and equal root.

EXAMPLES OF ROOTS:

  • Real roots of quadratic Equation:

x2-5x+6=0

Equating the formula into the discriminant of a quadratic equation,

b2-4ac=(-5)2-4*1*6=25-24=1

Using the Sridharacharya formula,

x=[-b(b2-4ac)]/2a

x=[-(-5)1]/2

x1=[-(-5)+1]/2=6/2=3

x2=[-(-5)-1]/2=4/2=2

Hence, the roots are 3 and 2, which are real roots of the quadratic equation.

 

  • Imaginary roots of quadratic Equation:

x2-6x+11=0

Equating the formula into the discriminant of a quadratic equation,

b2-4ac=(6)2-4*1*11=36-44=-8

Using the Sridharacharya formula,

x=[-b(b2-4ac)]/2a

x=[-(6)(-8)]/2

x1=[-(6)+(-8)]/2=[-6+8i]/2=2[-3+2i]/2=-3+2i

x1=[-(6)-(-8)]/2=[-6-8i]/2=2[-3-2i]/2=-3-2i

Therefore, the roots are (-3+2i) and (-3-2i), which are imaginary roots of quadratic equations.

CONCLUSION:

The primitive root is the smallest positive power that can rise over an integer, which is comparatively prime to another integer. The outcome of a primitive root can be a quadratic residue or a non-quadratic recipe. In either case, the quadratic equation must be simplified with the help of the Sridharacharya formula. The Sridharacharya formula equates a discriminant of the quadratic equation, which categorises the roots into five natures of roots, namely real roots, imaginary roots, rational roots, irrational roots, and equal roots. To better understand the topic of primitive roots in quadratic equations, one must have the basic knowledge of the prime numbers and the power raised to the numbers.