Integral Calculus Basics

Integral calculus can be used to find a function’s anti-derivatives. The function’s integrals are another name for these anti-derivatives. The technique of determining the anti-derivative of a function is known as integration. The technique of determining integrals is the inverse of determining derivatives.

The integral of a function represents a family of curves. Finding both derivatives and integrals is a requirement of basic calculus. We will go over the fundamentals of integrals and how to evaluate them in this article.

Integral Calculus

The values of the function discovered during the integration process are known as integrals. Obtaining f(x) from f'(x)is known as integration.

Integrals assign numbers to functions in a way that describes displacement and motion problems, area and volume problems, and other issues that arise when small data sets are combined.

Integral Calculus’s Fundamental Theorem

The first part of the theorem 

The first fundamental theorem of calculus – states that by integrating f with a variable bound of integration, one of the antiderivatives also known as an indefinite integral of a function f, say F, can be derived. This indicates that antiderivatives for continuous functions exist.

The second part of the theorem

The integral of a function f over some interval can be determined using any of its infinitely numerous antiderivatives, such as F, according to the second fundamental theorem of calculus. Since the integration constant C has an infinite number of options, there is an infinite number.

Integral Calculus Categories

The 2 types of integral calculus are as follows. They are as follows:

1. Indefinite integral

An indefinite integral is a function that takes the antiderivative of another function. The indefinite integral is not defined by upper and lower bounds. The indefinite integral represents the family of functions whose derivatives are f. It is impossible to change the distinction between any two family functions.

The integral key, which is normally used to obtain definite integrals, can be used to find indefinite integrals by simply deleting the integration limits. If f(x) has a value of F(x). Then this is what it looks like:

f(x)dx = F(x) + C

F(x) denotes Primitive or Antiderivative.

The Integrand is f(x), and the Integrating Agent is dx.

Integration’s variable is x.

The Constant of Integration is denoted by the letter C.

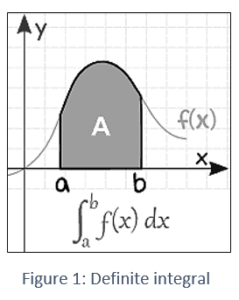
2. Definite integral

There are upper and lower limitations to a definite integral that is a start and an end value. x can only lie on a straight line. A definite integral is also known as a Riemann Integral when it is constrained to reside on the real line.

A representation of a definite integral is as follows:

∫^b_af(x)dx

Where, the lower and upper limits are a and b, respectively. f(x) is referred to as the integrand, while dx is referred to as the integrating agent.

Calculating the area enclosed by curves with coordinate axes is one of the uses of the definite integral.

Formulas for Integral Calculus

We have some integral formulas that are commonly used to calculate integrals. The following are some of the most important integral calculus formulas:

Constant rule: ∫kdx = kx + C

Sum rule: ∫fx±gxdx = ∫fxdx ± ∫gxdx

Power rule: ∫xⁿdx = (xⁿ⁺¹/n + 1) + C ,n ≠ -1

Log rule: ∫(1/x)dx = ln |x| + C,x≠0

Exponent rule: ∫a^kxdx = (a^kx/klna) + C,x≠0

Trigonometric rule:

∫sin xdx = x +C  

∫cos xdx = sin x +C  

∫tan xdx = ln |sec x| +C 

∫cot xdx = ln |sin x| +C 

Use of Integral Calculus

Integral calculus has two primary applications. The first is to calculate f from f’, and the second is to calculate the area under the curve.

The integral calculates the signed area, which is the total area above the x-axis minus the total area below the x-axis, because the general function f(x) is sometimes positive and sometimes negative. Positive/negative areas above/below the x-axis are counted by the integral.

Conclusion

We conclude in this article, that Integral calculus is an area of mathematics that deals with the theory, properties, and applications of integral calculus. The fundamental theorem of integral calculus relates the derivative and the integral, and the definite and indefinite integrals are two useful categories that are utilized to address many real-life situations. An integral is a function whose derivative is another function. Integration is used to calculate the volume of three-dimensional objects and the area of two-dimensional regions.