Independent Events

Throughout our lives, we will encounter a variety of random events. Some events are connected, and others have nothing to do with each other. For example, the toss of a coin, the roll of a dice, and the drawing of cards from a deck. Similarly, there are many types of events in probability such as dependent events, independent events, mutually exclusive events, etc. When there are dependent events, one event is dependent on the other. The events preceding and following an independent event have nothing to do with each other. In this article, we will explore independent events in depth.

What are Independent Events?

It is said the two events are independent events, meaning that what happens in one event is independent of what happens in the other. In the case of flipping a coin, one time you get heads and the next time tails, both of those events have nothing to do with each other, both of them independently yield either head or tail. We might take the example of drawing one card from a deck, and then drawing another from the same deck. This would mean that there would be one less card because a card has already been drawn. Therefore, it is classified as dependent events and not independent events. The outcomes of independent events can be similar.

Let us notate these events. Think about a situation in which the occurrence of event A does not depend on the occurrence of another event B. Prior to understanding how independent events are useful for probability, we will consider the formula for conditional probability. The probability of B such that the probability of A has already occurred can be expressed as P (B / A) when there are two events A and B. Consider the probability of event A such that the probability of event B has already occurred. Therefore, the conditional probability formula can be expressed as follows:

P (A / B) = P (A ⋂ B) / P (B) or P (B ⋂ A) / P (B)

As the name implies, this formula can only be used when the probability of two events is greater than 0 and that condition is fulfilled. In the event that P (A) is less than 0, the event is impossible and cannot occur. In the above formula, the combined probability of the two events is given as P (A ⋂ B).

According to the conditional probability event formula, if A and B are two separate events, then the independent probability of the events are written as follows:

P (A | B) = P (A)

If A and B are two events associated with the same random experiment, then the formula for independent events can be expressed as:

P (A ⋂ B) = P (B) . P (A)

Venn Diagram: Independents events

With the help of a Venn diagram, one can prove that independent events probability must meet certain conditions. This theorem states that if X and Y are independent events, then X’ and Y’ are also independent events, but because we have to prove it, let’s take A and B as independent events, such that P (X * Y) = P (X) . P(Y). In Venn diagram form, the following condition is:

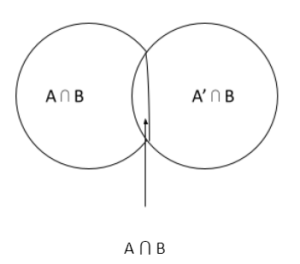
As can be seen from the Venn diagram above, the events X ⋂ Y and X ⋂ Y’ are both independent events, but together they create the event X, which can be expressed as follows:

X = (X ⋂ Y) U (X ⋂ Y’)

Therefore, the independent probability of the events will be:

P (X) = P [(X ⋂ Y) U (X ⋂ Y’)

How to Identify Independent Events?

So far, we have seen what independent events are and why they are useful in probability. Yet how can we tell that an event is independent before we apply the probability formula? Here is a method you can use in order to determine whether an event is dependent or independent:

Step 1: In the first place, it’s important to check if the events can actually happen because the events will only occur if the possibility of two happening at the same time is greater than 0.

Step 2: In terms of the outcome, you need to ensure that one event does not affect the other.

Step 3: The formula for independent events probability can be used once you are sure the events are independent.

Conclusion

The probability principle is applied to a lot of our everyday activities, including driving a car and using a handheld device. Independent events simply mean that one event has nothing to do with the other. Probability involves many concepts, among which is the concept of independent events, the one which we discussed in this article. Along with seeing the difference between dependent and independent events we also saw the formula for independent events and when and how to use the independent events probability formula. We also saw the independent events theorem is proved using Venn’s diagram. In general, independent events are a fundamental concept in probability and can be useful and applicable to everyday life as well.