Hyperbolic Functions

Hyperbolic functions have the characteristics of trigonometric functions and are used in many mathematics problems. They are also commonly referred to as hyperbolic trigonometric functions. 

Usually, these functions are used while calculating the angles and distances in hyperbolic geometry. They are also used while solving linear differential equations and Laplace’s equations in the cartesian coordinates. 

In this article, we will define hyperbolic functions and their properties in simple words. We will cover both the basic and advanced features of hyperbolic functions.

Hyperbolic Functions Definition:

Hyperbolic functions were introduced by Vincenzo Riccati and Johann Heinrich Lambert in the 1760s. These functions are analogous to trigonometric functions. 

The main difference between the two is that the hyperbola is used in hyperbolic functions rather than the circle which is used in trigonometric functions. 

This means that a graph of a hyperbolic function represents a rectangular hyperbola. These functions are defined using algebraic expressions. You will mainly find these six hyperbolic functions:

1. sinh x
2. cosh x
3. tanh x
4. coth x
5. cosech x
6. sech x

Hyperbolic Functions Formulas:

Domain and Range of Hyperbolic Functions: 

Properties of Hyperbolic Functions:

The size of a hyperbolic angle is double the area of its hyperbolic sector. You can also define hyperbolic functions like the legs of a right triangle covering the sector.

The theory of functions of a complex variable which studies the functions of a complex variable states that hyperbolic functions can be seen as the imaginary parts of sine and cosine.

This means that hyperbolic sine and the hyperbolic cosine are integral or entire functions.

Now, you may ask what is an entire function? Great question! 

In terms of complex analysis, an entire function is a complex-valued function that is holomorphic (can be differentiated at each and every point of its domain) on the whole complex plane.

The other hyperbolic functions: tanh x, coth x, cosech x and sech x are meromorphic (a complex variable that is analytic everywhere in a region) in the whole complex plane.

The other properties of these functions are similar to the trigonometric functions.

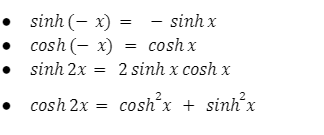
Derivatives of Hyperbolic Functions:

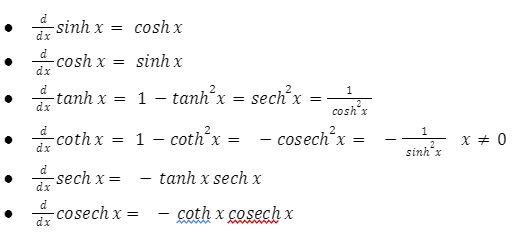
Hyperbolic functions satisfy many trigonometric identities. According to Osborn’s rule, one can easily convert any trigonometric identity into a hyperbolic identity for , 2, 3 or and . You can do this by following these 2 steps given below:

1. First, expand the functions in terms of integral powers of sines and cosines.
2. Then, simply change the sign of every term containing a product of two sinh functions.

Odd and even functions:

• sinh(-x)= -sinh x
• cosh(-x)= cosh  x

Hence,

• tanh(-x)= -tanh x
• coth(-x)= -coth x
• sech(-x)= sech x
• cosech(-x)= -cosech x

Inverse Hyperbolic Functions:

Now that we have understood the meaning and properties of hyperbolic functions it’s time to understand its inverse. 

In simple words, the inverse hyperbolic functions represent the inverse functions of the hyperbolic functions. The corresponding inverse hyperbolic function gives the corresponding hyperbolic angle.

These functions are as follows:

Conclusion:

Hyperbolic functions are the important mathematical concept that is commonly used in hyperbolic geometry for estimating angles and distances. They are similar to trigonometric functions. 

Although both the hyperbolic and trigonometric functions serve a different purpose. It is important to know the meaning of hyperbolic functions along with their properties and formulas.