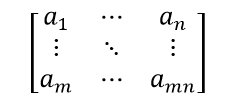CSIR NET EXAM » CSIR UGC-NET Exam Study Materials » Mathematical Sciences » determinant of matrices

determinant of matrices

tailed understanding of the Determinant of Matrices.Meta description - Everything you need to know about the Determinant of Matrices and other related topics in detail. In the domain of linear algebra, determinants and matrices have been used to fix linear equations. Cramer's rule is implemented to a series of non-linear equations.

Determinant of matrices is mostly computed for a series of square matrices. When the condition of a matrix is zero, then it is referred to as singular, and in the instance of one, it is made reference to unimodular. It is required that the determinants or the conditions of the matrix have to be non-singular. It means that it should have a value and must be not a zero. These should be the determinants for the entire series of equations and they should have a unique solution.

Definition Of Matrices

Determinant of matrices is a commanded rectangular array of statistics used to represent linear equations. A matrix is made up of rows and columns. We can also accomplish arithmetic computations on matrices including addition, subtraction, and matrix complex multiplication. If the number of rows is denoted as m and the number of columns is denoted as n, the matrix is represented as m × n matrix. This is the Matrices Definition.

Types Of Matrices

Matrixes come in different types. Let’s look at some examples of various types of matrices.

i.  Zero Matrix: 

 

000

000

000

 

ii. Identity Matrix:

 

100

010

001

 

Iii. Symmetric Matrix

 

3

2

-1

2

0

5

-1

4

6

 

iv. Diagonal Matrix:

 

800

060

004

 

v. Upper Triangular Matrix:

 

5

0

0

-1

4

0

6

2

2

 

vi. Lower Triangular Matrix:

                                  

4

6

2

0

3

-1

0

0

2

 

Inverse Of A Matrix

In most cases, the inverse of a matrix is characterized for square matrices. There is an inverse matrix for every m x n square matrix. If B is the square matrix, then B-1 is the inverse of B and fulfils the following property:

Where I is the Identity matrix, BB-1 = B-1B = I.

Also, the determinant of the square matrix cannot be zero in this instance.

Transpose Of Matrix Representation:

A matrix’s transpose can be ascertained by replacing rows for columns. If B is a matrix, then BT represents the matrix’s transpose.

Assume we have a 3×3 matrix, say B, and the transpose of B, i.e. BT, is given by

 

B

 

=

6

2

5

3

9

7

5

4

3

 

B

T=

6

3

5

2

9

4

5

7

3

If the given square matrix is symmetric, then the matrix B should be equal to BT. It denotes that B = BT.

Matrix Determinants

The determinants play a significant role in attempting to solve a set of linear equations and discovering the inverse of a matrix. Let us now look at how to find the determinant of a 3×3 matrix. If B is a matrix, the determinant of b is typically represented by det (B) or |B|.

How to find Determinants for 3×3 matrix: Let us assume a 3×3 square matrix as follows: 

 

B

 

=

2

4

6

3

6

9

4

8

9

Then |B| is denoted as follows

=

2

4

6

3

6

9

4

8

9

 Conclusion 

We discussed definitions of matrices and the different types of matrices along with their properties and examples and other related topics through the study material notes on Determinant Of Matrices. We also discussed Matrix Determinants to give you proper knowledge. 

The determinant is a scalar parameter in mathematics that is a component of the submissions of a square matrix. It facilitates the characterization of certain properties of the matrix and the linear map defined by the matrix. A matrix B’s determinant is denoted by det(B), det B, or |B|. The determinant is a unique identification number that could be determined using a matrix. The matrices must be square with an exact number of rows and columns.