Profile
Settings
Refer your friends
Sign out
The greatest common factor between two or more numbers is known as the HCF. The “Greatest Common Divisor ” is another name for it (GCD). The HCF of 18 and 48, for example, is 6, because 6 is the greatest integer that can completely divide both numbers. Similarly, the smallest number that is a common multiple of the supplied numbers is the least common multiple (LCM) of two or more numbers. There are two generally used methods for determining HCF and LCM. Learning HCF and LCM in mathematics is critical since it aids us in solving day-to-day difficulties involving grouping and sharing. Let’s look at the many ways for calculating the HCF and LCM of numbers.
Ways to Find LCM and HCF
There are two main ways to find HCF and LCM-
- Prime Factorization method
- Division method
HCF and LCM Formulas
HCF LCM = a b is the LCM and HCF formula for two numbers ‘a’ and ‘b’. To put it another way, the LCM and HCF formula asserts that the product of any two numbers is the sum of their HCF and LCM.
To compute the LCM and HCF formula using the prime factorization method, we must first discover the prime factors of the supplied numbers using either the ladder approach or the factor tree method. Then, using the steps outlined below, we can determine the HCF and LCM values.
HCF of two numbers by Prime Factorization
We find the prime factors of the supplied numbers to find the HCF of those numbers using prime factorization. We find the product of the prime factors that are common to each of the given numbers after we’ve found the factors. Let’s use the prime factorization method to find the HCF of 50 and 75, for example.
50 = 2 x 5 x 5 are the prime factors.
75 = 3 x 5 x 5 are the prime factors.
The common factor between 50 and 75 is 5 x 5. As a result, the HCF of (50, 75) = 25.
LCM of two numbers using Prime Factorization
Following the procedures below, we can calculate the LCM of any two numbers using the prime factorization method:
Step 1: Make a list of the prime factors of the provided numbers, noting which ones are common.
Step 2: The LCM of the given numbers is equal to the product of the numbers’ common prime factors and unusual prime factors.
Note that common components will only be mentioned once.
Let’s use prime factorization to find the LCM of 160 and 90.
Step 1: The prime factors of 160 = 2 x 2 x 2 x 2 x 2 x 2 x 5 and 90 = 2 x 3 x 3 x 3 x 5 are added together.
Step 2: Add all the prime factors together = Common prime factors (2 x 5) Uncommon prime factors (2 x 2 x 2 x 2 x 3 x 3) = 1440.
As a result, the LCM of 160 and 90 is 1440.
HCF of two numbers using Division Method
HCF and LCM can be calculated in two ways using the division method.
Follow the steps below to find the HCF using the division method:
Step 1: To begin, divide the larger number by the smaller number and examine the remainder.
Step 2: Perform the division again, using the residual of the previous step as the divisor and the divisor of the previous step as the dividend.
Step 3: Continue dividing until the remainder is not equal to zero.
Step 4: The HCF of the given numbers will be the final divisor.
For example, to find the HCF of 144 and 160.
Since 160>144, so the dividend will be 160 and the divisor will be 144.
By using the division method, we get:
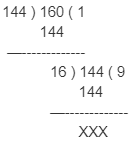
As a result, the largest number that divides 160 and 144 is 16.
As a result, HCF (144, 160) = 16.
LCM of two numbers using Division Method
We divide the numbers using prime numbers and terminate the division process when we receive only 1 in the final row to find the LCM of numbers using the division method.
Step 1: Multiply the numbers by the smallest prime number, ensuring that the prime number divides at least one of the given numbers.
Step 2: Write the quotients just beneath the next row’s numbers.
Step 3: Assume the above quotients are the new dividends for the following division step.
Step 4: Consider another prime number that divides at least one of the dividends perfectly.
Step 5: Repeat Steps 1–5 until we have 1 in the last row
For example, to find the LCM of 60 and 45
2 | 60, 45
2 | 30, 45
2 | 15, 45
2 | 5, 15
2 | 5, 5
5 | 1, 1
Hence, LCM of 60 and 45 is 2 × 2 x 3 × 3 × 5 = 180
Conclusion
The main HCF and LCM formula is that “The product of any two numbers’ H.C.F. and L.C.M. is always the same as the product of those two numbers”. When we wish to break things into smaller sections, we use it to divide things into smaller sections, to organise things into rows or groups, to distribute more products to large groups, and to figure out how many people we need to invite, and so on.
