Profile
Settings
Refer your friends
Sign out
The combination is indeed the process of selecting items from a group of elements without regard to their selection sequence. When the selection sequence is used as a criterion in a selection procedure, it is referred to as a permutation. The combination is a sort of permutation selection wherein the order of the items is irrelevant. As a result, the number of permutations for picking ‘k’ components out of ‘n’ elements is always more than the number of combinations.
There are additionally two sorts of combinations (the order of which is irrelevant)
Repetition is permitted, such as in the case of money in your pocket (5,5,5,10,10)
There will be no repetition, such as in lottery numbers (2,14,15,27,30,33)
Repetition in Combinations
These are the most difficult to explain, so we’ll return to them later.
Non-repetitive combinations
The way lotteries function is as follows. The numbers are picked one by one, and we win if we have the lucky numbers (in any sequence)!
The simplest way to describe it is as follows:
Assume that the order is important (i.e., permutations),
Then change it such that the order is irrelevant.
Combination formula
The method of calculating the number of alternative configurations by picking only a few objects from a collection with no repetition in mathematics is as follows:
Where:
n – the total elements
k – the number of objects that have been selected
! – factorial
A product of all positive integers smaller or equal to the number preceding the factorial sign is known as a factorial (noted as “!”). 3! = 1 x 2 x 3 = 6 is an example.
It’s worth noting that the formula above can only be utilised when objects from a set are chosen without being repeated.
Combination Properties
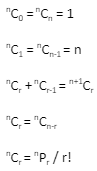
Facts to Know About the Combination Formula
Permutations and combinations are commonly employed in probability, genetic engineering, and life sciences problems requiring the selection and organisation of items.
Because the sequence of the integers affects so much, a ‘Combination Lock’ should be named a ‘Permutation Lock.’ If it’s a combination lock, though, the sequence of the numbers shouldn’t matter. (Hint: remember what combo definition means.)
Basic concepts of Permutation and Combination
A permutation is a mathematical computation that determines the number of different ways a given set may be organised, with the order of the arrangements being important.
A basic concept of permutation and combination is a mathematical approach for calculating the number of potential arrangements in a set of things when the order of the items is irrelevant. You can choose the components in any order in combinations. Permutations and combinations are often mistaken.
Permutations vs Combinations: What’s the Difference?
It is not even if there isn’t repetition that distinguishes Permutations and Combinations. Neither of them permits for the same thing to happen twice. The distinction between the two isn’t whether the order is critical. If you’re having trouble repeating objects, you’ll need to apply the Fundamental Counting Principle instead of Permutations or Combinations.
Conclusion
The combination is the process of categorising some or all items into groups, regardless of their organisation. The combination is the classification of given things into groupings in simple words. Sequencing is the primary distinction between permutation and combination. In permutation, we must be concerned with the order in which items are ordered. In combination, though, we don’t need to worry about the order because we’ll be grouping the provided items regardless of their order. The symbol for combination is nCr or C (n, r), where ‘n’ is the provided number of objects and ‘r’ is the number of things taken at once. For instance, if somehow the total number of things is 6, we must categorise them into groups by picking four objects at a time; the combination is 6C4 or C. (6, 4).
