Theory on Gauss’ Law

In this article, we will read about one of the most interesting topics of electromagnetism. In 1773, for the very first time, Joseph Louis Lagrange introduced this law and later was given by Carl Friedrich Gauss in 1835. This law states that “the total electric flux of a closed surface is directly proportional to the net electric charge in an enclosed surface”. Gauss’s law is also named Gauss’s flux theorem(commonly Gauss’s). The gauss law formula can be written as:

                                                 ϕE = Q/εo

Where Q is the total charge on the surface and ε0 is the electric constant. SI unit of gauss law is Nm2/C.

Application Of Gauss’s Law:

We know very well about Gauss’s law from the last paragraph, but still, we don’t know where we have to apply this law in our daily life, and that is the biggest query in our mind? It is not as hard as we think. Gauss’s law can be used to simplify the composite electrostatic problems involving different symmetries such as cylindrical, spherical, or planar symmetry. In easy words, we can say that it is used to simplify the evaluation of electric fields. There are some more applications on Gauss’s law given below.

1. An infinitely long wire which is straight & charged produces an electric field:

 Consider an infinitely long, evenly electrified cable with length ‘l’. Its corresponding linear charge density ‘λ’ is constant. The electric flux through curved surface = ∮Eds cos Ө.

Where, (ds=2πrl),( Ө=0; cosӨ=1). So total flux through the gaussian surface is given below,

Φ=E (2πrl)

And the net charge enclosed by Gaussian surface is q = λl

∴ By Gauss’s law,

 E×(2πrl) = λl/εo 

or E = λ/2πεor

2. An infinitely charged plane sheet produces an electric field;

Consider an infinite plane sheet having charge density ‘σ’. Let P be a position at a particular distance ‘r’ from the corresponding sheet. Total flux through the closed surface is given by

Φ=[∮E.ds]+[∮E.ds]                                   (∵Ө=0o,cosӨ=1)

 Φ=EA+EA=2EA 

And the net positive charge q within the surface as per Gauss’s Law is q=σA

∴ By Gauss’s law,

2EA=σA/εo or E= σ/2εo

3. Electric field due to two parallel charged sheets: 

As indicated in the diagram, Take into consideration two plane parallel limitless sheets with equivalent and opposing charge densities +σ and -σ. The electric field on a simple sheet of charge has a magnitude of E=σ/2εo and works perpendicular to the sheet, exerted outward (as the charge is positive) and inward (as the charge is negative).

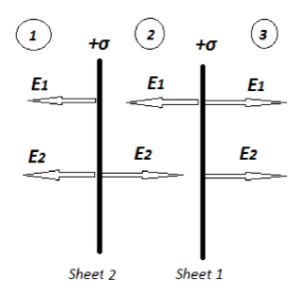
(1)  Region I  is outside the sheets; the resultant field around region III is,

                                                     E= σ/εo–  σ/εo = 0

(2) Region II is in between the sheets; the resultant field around region II is,

                                                     E= σ/εo

(3) Region III is outside the sheets; the resultant field around region III is,

                                                      E= σ/εo–  σ/εo = 0

4. Electric field due to a uniformly charged spherical shell:

CASE1: At a point outside the shell.

 Consider a charged shell of radius R. Let P be a point  outside the shell at a distance r from the center O. The flux crossing the Gaussian surface in an outward direction is,

                                       Φ = ∮E.ds = ∮E(4πr2)

 ∴ By Gauss’s law,

                                 E(4πr2) = q/εo or E = q/4πr2εo

CASE2: At a point on the surface.

                                       E = q/4πR2εo                 (∵r = R )

CASE3: Inside the shell, at a certain position:

 Consider a point ‘P’ inside the shell at a distance ‘r’ from the centre of the shell. The flux crossing the surface of the Gaussian in a direction outwards is,

                                          Φ = ∮E.ds = ∮E(4πr)

Because the Gaussian surface does not contain any charge,

 ∴ By Gauss’s law,

                                     E × 4πr2 = q/εo = 0                            (∵ E = 0 )               

Conclusion

The electric field is the most fundamental idea in understanding electricity. In general, the electric field of a surface is computed using Coulomb’s equation; however, understanding the notion of Gauss law is required to estimate the current distribution in a closed path. It explains how an electric charge is confined in a closed path or how an electric charge is present in a closed surface that is enclosed. The total charge contained in a closed path is proportional to the total flux encompassed by the surface, according to the Gauss theorem.