THE KINETIC THEORY OF AN IDEAL GAS

In Physics, ideal gas is defined as the gas which obeys or follows the previously defined gas laws. Therefore, it becomes a necessary task to understand all the concepts related to the ideal gas, the gas laws, and how they affect when certain parameters are embedded in a change like increasing or decreasing temperature, checking the pressure of the gas, etc.

By Ideal gas, we mean a special type of gas that is hypothetical and behaves differently from the real gases which are present around us, in the atmosphere. We will be discussing the fundamental theory related to the ideal gases and how they behave with changes in certain factors like temperature and pressure. 

What exactly is an Ideal gas?

• The word ‘ideal’ in English means ‘perfect’. While dealing with modern sciences, Ideal gas is defined on a certain basis.
• Any gas can be called an ‘Ideal Gas’ only and only when it obeys the gas

• laws that are stated to determine the behaviour of gases. Simply for a gas to be Ideal, it has to strictly abide by the Gas Laws. 

The main postulates or points of gas laws are as follows: 

• • The first postulate states that an Ideal gas will have molecules with negligible forces of attraction. In other words, the forces of attraction or repulsion between the molecules are zero.
  • The second postulate states that the particle size or the molecule size of an ideal gas is negligible or we can say that the size of the gas molecules is so small that it can be treated as zero. So, for this postulate, it can be summarised that for an ideal gas, the molecule size is zero.

Kinetic Theory of An Ideal Gas

Since the definition of an ideal gas is very clear, we can now discuss another important theory popularly known as ‘The Kinetic Theory of Gases.’

This theory plays an important role in determining the behaviour of gases and their relation to temperature and pressure.

This law was put forward by the British scientist James Clerk Maxwell and the Austrian Physicist Ludwig Boltzmann during the late 19th century.

Since gas is one of the physical states of matter and matter consists of atoms and molecules, this theory talks about the molecules of gases.

This theory has many postulates or statements.

• We assume that the molecules are moving in a random fashion and in all directions.
• All the molecules of any particular ideal gas will have the common Avogadro’s number.
• The next point states that the molecules will not exert any force of attraction or repulsion on each other, excluding the case of collisions.
• The fourth point talks about the size of gas molecules. The gaseous molecules are so small that they tend to have negligible forces, zero interaction amongst them, even if the temperature and pressure are changed.

• Lastly, the molecules of ideal gases will always experience collisions whose nature will be ‘perfectly elastic. Since they are gaseous, small molecules, they will collide either with the containers’ walls or against each other.
• Due to the collisions of gaseous molecules, they will move with a certain velocity but the fact is the momentum and the kinetic energy of the molecules will remain constant and conserved when a collision occurs.

The pressure of an Ideal gas

Gas will always show changes when there is a change in pressure but for the pressure of an ideal gas, it is a little different.

We will be deriving the expression for the total pressure exerted by the molecules of an ideal gas when placed in a closed vessel or solid container.

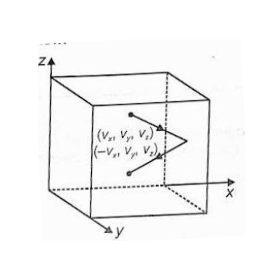
Let us consider the case of a solid cube having side ‘l’. We will place or fill the cube with the ideal gas. For further solving, we need to find out the coordinates of the cube. See the figure below for reference.

We will make use of one of the assumptions from the kinetic theory of gases, about the collisions being perfectly elastic, and hence, we can determine the velocity for the molecule across the three axes namely Vx, Vy, Vz after the collision.

When gaseous molecules will collide with a certain velocity, there will be a change in the linear momentum of the molecule which is given below:

-mvx-(mvx)=-2mvx

Note the time for which molecules hit the walls of the cube. The number of the times the molecules effectively hit the wall is given as: (12Avxt)n

The total momentum for the gaseous molecules will be:

p=12(Avxt)n2mvx

The molecules of gas will be exerting a force on the cube walls which is given by:

P=pAt=nmvx2

So far we were calculating the expression for a molecule of gas for one axis. We have to find the expression for total pressure for the three axes as gas molecules are moving and colliding randomly.

The final expression of pressure exerted of an ideal gas is: 

P=13nmv2

Where v is the speed.

Kinetic Interpretation of Temperature

We will derive an expression for the Kinetic interpretation of temperature. Remember that kinetic energy is directly proportional to the temperature of the gas.

The kinetic interpretation of temperature is given as:

E=32NkBT

Or EN=1/2m/v2=3/2kBT

Conclusion 

In this module, we learned about the definition of an ideal gas and how it is incorporated in the world of Physics. Any gas can be called an ‘Ideal Gas’ only and only when it obeys the Gas. Laws that are stated to determine the behaviour of gases. Simply for a gas to be Ideal, it has to strictly abide by the Gas Laws. ‘The Kinetic Theory of Gases’ plays an important role in determining the behaviour of gases and their relation to temperature and pressure. This law was put forward by the British scientist James Clerk Maxwell and the Austrian Physicist Ludwig Boltzmann during the late 19th century.