System of particles and rotational motion

An inflexible body is categorised as one with a perfectly regular and definite shape. The distances between all sets of particles remain unchanged.

In translational movement, at any given moment, all particles of the entity have the same velocity.

When an inflexible body rotates about a fixed axis, every particle of the inflexible body moves in a circular motion. The movement of an inflexible body that is fixed at its centre is either a pure translation or a combination of translation and rotation. Rotation is the movement of an inflexible body that is fixed or pivoted at a point.

Centre of mass

• This is the imaginary point where the entire mass of a system can be assumed to be consolidated.

Motion of COM

• The centre of mass of a system of particles moves as if all the mass was centralised and all the external forces were applied at that point.

•  The translational component of the motion is the movement centre of mass, by taking the mass of the entire system to be consolidated at the centre of mass and all the external forces on the system to be working at the centre of mass in it.

Linear momentum of system of particles

• In the system, the total momentum of all particles is equal to the multiplication of the system’s total mass and the velocity of its centre of mass.

P = P1 + P2 + …. + Pn 

P = M1V1 + M2V2 + …. + MnVn

P = MV

P – momentum of Particles in a system,

M – mass of the system

V – velocity of the centre of mass

 The second law of Newton extended to a system of particles: dP/dt =force external

• When the external force is 0 which means the total external force applied on a system is 0, the total linear momentum of the system is constant (dP/dt = 0 => P = constant). Also, the velocity of the centre of mass = constant 

 Example – A bullet m mass is fired at a velocity of v1 and penetrates a block of mass M, initially at rest and on a frictionless surface. 

What is the final velocity of the block?

Solution: Suppose we take bullet and block as a system, then no external force is working on it. So we can conserve momentum. 

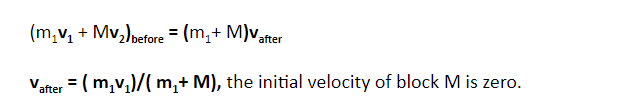
Angular velocity & its relation with linear velocity

In rotation, each particle of the body moves around in a circle. Angular velocity is defined as the angular displacement of the particle around its axis in a unit of time.

 The average angular velocity = ΔΘ/Δt

• The Instantaneous angular velocity is ω = dΘ / dt

• We know v = ω r, in which v is the linear velocity of a particle moving in a circle of radius r.

• Angular acceleration is known as the rate of change of angular velocity with respect to time.

• α = dω / dt

Torque & angular momentum

• The rotational analogue of force is a moment of force (Torque).

• Suppose a single particle is present at point P and a force is applied at point P with reference to origin O is represented by position vector r, the moment of the force on that particle is known as torque=r  F sin Θ

• Torque – vector quantity.

• The quantity angular momentum is the rotational analogue of linear momentum.

• It could also be referred to as a moment of (linear) momentum.

• L = r × p

Conservation of angular momentum

•  When the total external torque on the system is 0, the total angular momentum of the system is conserved.

• Suppose the external torque becomes 0, then d(L)/dt = 0 means L is constant

Equilibrium of inflexible body

• If a force alters the translational state of the motion of the rigid body, then the total linear momentum of the body alters.

• The total angular momentum changes if a torque changes the rotational state of motion of the rigid body. An inflexible body is in mechanical equilibrium if its linear momentum and angular momentum do not change with time.

  • Total force zero for translational equilibrium

• Total torque zero for rotational equilibrium

Moment of inertia

• The moment of inertia that is represented by (I) is known as the analogue of mass in the rotational motion of the body.

• The rotational inertia of a body is the moment of inertia around the axis of rotation which resists the change in rotational movement of the inflexible body. It depends on the mass of the body, shape, and also size.

• I = M k2, in which k is known as the radius of gyration.

Rolling motion

The rolling motion of an inflexible body is a composition of rotation and translation.

In a rolling body, there are two kinds of velocity

The first one is Translational which is known as the velocity of the centre of mass.

• The second one is rotational motion due to linear velocity.

• Kinetic Energy of Rolling Motion

• KErolling = KEtranslation + KErotation

Conclusion

Rotational motion is more complex than linear motion. An inflexible body has a perfectly regular and definite shape. The distances between all sets of particles remain unchanged. In the mechanics of rotating bodies, numerous equations are similar to the motion equations for linear motion. In rotational movement, the particles of the entity, while moving, follow a circular path. Every particle in the inflexible body proceeds along a circular path along a plane perpendicular to the axis and has its centre on the same axis.