Profile
Settings
Refer your friends
Sign out
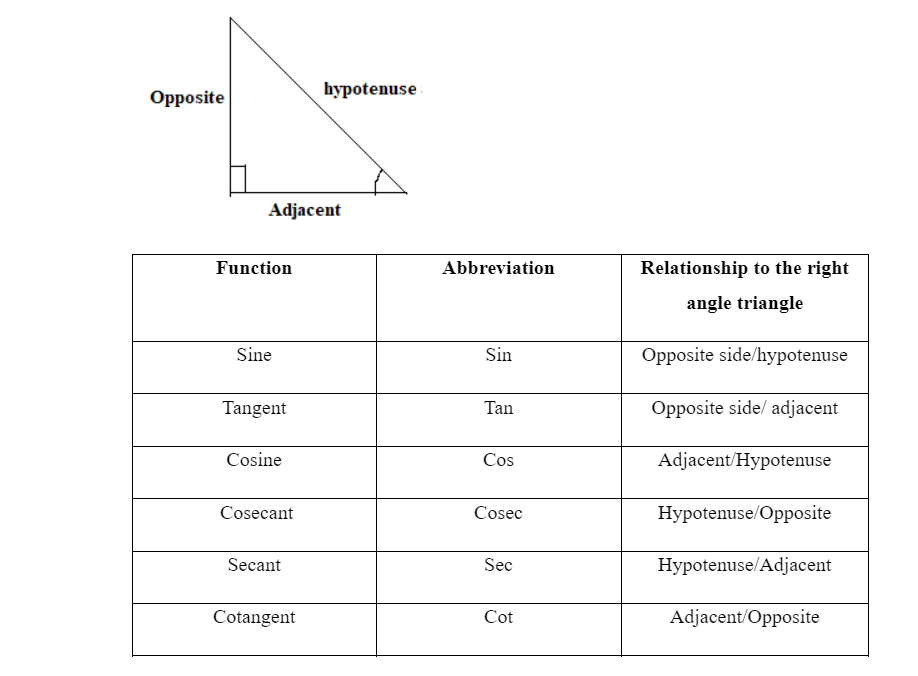
Trigonometry is the branch of Mathematics that involves the study of the length and angle relationships of triangles. Usually, it is associated with a right-angled triangle, in which one of the angles is always a 90-degree angle. Many geometric calculations can be easily solved by using the table of trigonometric functions and formulas. Trigonometric ratios help to find the value of the standard angles such as 0°, 30°, 45°, 60° and 90°.
The trigonometric ratios are contained in a trigonometric table such as cosine, sine, cosecant, tangent, cotangent, secant. The abbreviation used for the s trigonometric ratios is cos, sin, sec, cosec, cot, and tan. It is convenient and easy to learn the trigonometric table and the table can also be referred to solve problems related to trigonometry. The trigonometry table is not only used for solving problems related to it but also used for engineering projects, and other science-related activities and are also used in navigation.
Trigonometric values
Trigonometric values are determined as the values on an angle in a right-angle triangle in terms of trigonometric ratios sin , cos , tan , cot , cosec , sec.
Trigonometric values
sin ϴ = opposite/hypotenuse
cos ϴ = adjacent/hypotenuse
tan ϴ = opposite/adjacent
cosec ϴ= hypotenuse/opposite
sec ϴ = hypotenuse/adjacent
cot ϴ adjacent/opposite
Check out this detailed video for Inverse Trigonometric Functions –
Tricks to learn Trigonometric Table
Learning a trigonometry table is very easy if one knows the formula properly. The table of trigonometry depends on the trigonometric formula. The basic trigonometric formula before going further is:
sin ϴ = 1/cosec ϴ
cos ϴ = 1/sec ϴ
sec ϴ = 1/cos ϴ
cosec ϴ = 1/sin ϴ
tan ϴ = 1/ cot ϴ
cot ϴ = 1/ tan ϴ
Steps to Create a Trigonometric Table
Step 1
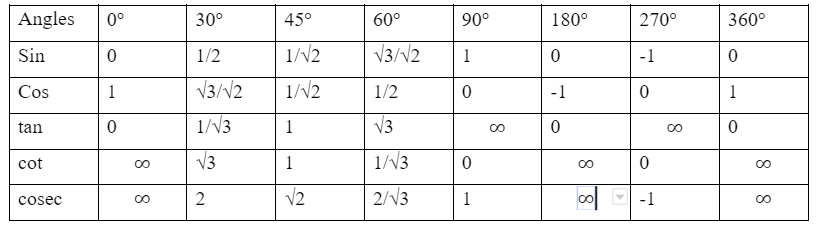
A table must be created with the top row having the standard angles in it, the angles like 0°, 30°, 45°, 60°, 90°, 180°, 270°, 360°, and the first column on the left-hand side must contain with every trigonometric function like cos, sin cot, tan, sec and cosec.
Step 2
Getting the sin value
For finding the value of all the degrees in sin, one needs to divide the under the root of 0,1,2,3,4 respectively. For example, 0/4 = 0
Therefore the trigonometric table of sin will be as follows.
|
Angles |
0° |
30° |
45° |
60° |
90° |
180° |
270° |
360° |
|
Sin |
0 |
1/2 |
1/√2 |
√3/√2 |
1 |
0 |
-1 |
0 |
Step 3
Getting the cos-value
The cos angles values are just the reverse of sin angles values. For getting the cos-value, one needs to divide by 4 in the reverse sequence of the sin-value. For example, to get the value of cos 0°, the step should be 4/4 = 1.
Therefore, the trigonometric table of cos will be as follows.
|
Angles |
0° |
30° |
45° |
60° |
90° |
180° |
270° |
360° |
|
Cos |
1 |
√3/√2 |
1/√2 |
1/2 |
0 |
-1 |
0 |
1 |
Step 4
Getting the tan value
The tan angle values are the division of sin angle values and cos angle values. That is tan = sin/cos. For example, if one tries to find the value of tan 0°, then one must do as follows
tan 0° = sin 0°/cos 0°
tan 0° = 0/1 = 0
Therefore, the trigonometric table of tan will be as follows.
|
Angles |
0° |
30° |
45° |
60° |
90° |
180° |
270° |
360° |
|
tan |
0 |
1/√3 |
1 |
√3 |
0 |
0 |
Step 5
Getting the cot value
The cot angle values are just inversely proportional to the value of tan. For example, the value of cot 0° can be calculated as the 1 divided by the value of tan 0°, to find the value of cot 0° one needs to do the following
Cot 0° = 1/0 = not defined or infinite
Therefore, the trigonometric table of the cot will be as follows.
|
Angles |
0° |
30° |
45° |
60° |
90° |
180° |
270° |
360° |
|
cot |
√3 |
1 |
1/√3 |
0 |
0 |
Step 6
Getting the cosec value
The cosec angle values are just the reverse of the value of sin at all the degrees respectively. For example,
cosec 0° = 1/0 = Not defined or infinite
Therefore, the trigonometric table of cosec will be as follows.
|
Angles |
0° |
30° |
45° |
60° |
90° |
180° |
270° |
360° |
|
cosec |
2 |
√2 |
2/√3 |
1 |
-1 |
Step 7
Getting sec value
The sec angle values are just the inverse of cos angle values at all the degrees respectively. For example, sec 0° = 1/1 = 1
Therefore, the trigonometric table of sec value is as follows.
|
Angles |
0° |
30° |
45° |
60° |
90° |
180° |
270° |
360° |
|
sec |
1 |
2√3 |
√2 |
2 |
-1 |
1 |
Example:
What is the value of 4360° +3 30° -230° -3460° ?
Solution:
43*(3)2+3*(3/2)2-2*(23/3)2-34*(3/3)2
=43*3+3*34-2*129-34*39
=4+94-83-1/4
=103
=313
