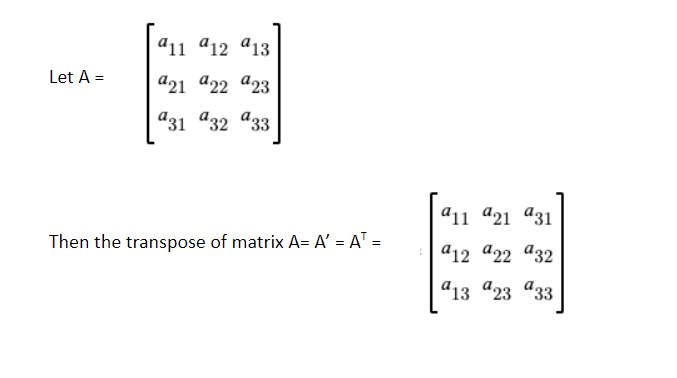Transpose of A Matrix

A matrix is a rectangular array of numbers that are arranged in rows and columns. There are several types of matrices such as row and column matrix, diagonal matrix, vertical and horizontal matrix, upper and lower triangular matrix, square matrix, zero or null matrix, and symmetric and skew-symmetric matrix, amongst many others.

The transpose of a matrix is obtained by interchanging its rows with its columns or its columns with its rows. Therefore, the transpose of a matrix will be obtained if the elements in the first row of matrix A are written in the first column, the elements in the second row are written in the second column, and so on.

Transpose of a matrix 

• The transpose of a matrix is obtained by interchanging its rows with its columns or its columns with its rows. Therefore, the transpose of a matrix will be obtained if the elements in the first row of matrix A are written in the first column, the elements in the second row are written in the second column, and so on.

• Let A be a matrix. Then, matrix A’s transpose will be denoted by either A’ or AT. 

• If A = (aij) m × n, then ‘ A’ = (aji) n × m. 

Transpose of a 2 × 2 matrix 

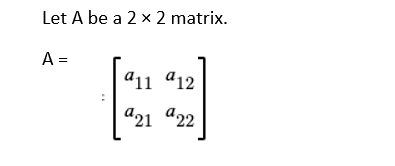
Then the transpose of A = A’ = AT =         

For example, C =

Then the transpose of matrix C  C’ =

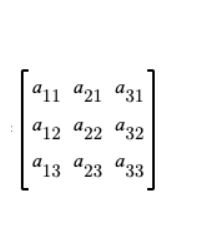
Transpose of a 3 × 3 matrix  

Let A be a 3 × 3 matrix. 

Let A = 

Then the transpose of matrix A= A’ = AT =

Properties of transpose of a matrix 

The properties of a transpose of a matrix are:

• For a square matrix, say A, of order n, (A’)’ = A.

• For two square matrices, say A and B, of order n, (A + B)’ = A’ + B’ 

• The multiplication of a matrix with any constant property states that if a matrix is multiplied with a constant and its transpose is determined, then the matrix obtained will be equal to the transpose of the original matrix, which is multiplied with a constant. In simpler (kA)’ = kA’, where k is a constant.

• The transpose of the product of two matrices of order n is equal to the product of their transpose in the reverse order.

Transpose of a column matrix

• A column matrix is one of several types of matrices. A column matrix is a matrix that has only one column and n numbers of rows.

• For example, A = 99 199 299 is an example of a column matrix.

• Let A = [a11 a21 a31], then the transpose of A = A’ = AT = a11 a21 a31.

• For example, let A = 99 199 299 , then AT = [99 199 299 ].

Transpose of a row matrix

• A row matrix is a matrix that has only one row and n numbers of columns.

• Let A = a11 a12 a13 a14 be a row matrix, then the transpose of A will be = A’ = a11 a12 a13 a14.

• For example, A = 100 1000 10000, then the transpose of A = A’ = 100 1000 10000 .

• Conjugate transpose of a matrix refers to a matrix resulting from transposing a matrix and replacing all of its elements with its conjugates.

• The transpose of a conjugate matrix can also be described as a matrix that is obtained by transposing the complex conjugate entries of the original matrix.

• The conjugate transpose of a matrix is also called a hermitian adjoint or hermitian transpose, adjugate matrix, or an adjoint matrix.

• Conjugate transposition of a matrix follows the properties of both transposition and conjugation.

Transpose of different types of matrices 

Symmetric matrix

• A square matrix is called a symmetric matrix if, after transposing, the values of the rows and columns remain unchanged. 

• For example, 

A = 

and 

AT =

• In this case, A is a symmetric matrix because after transposing its value, the entries in the rows and columns remained unchanged.

Diagonal matrix 

• A diagonal matrix is a matrix where all of the non-diagonal entries are zero. 

Let us find the transposed matrix of the diagonal matrix. For example, 

A is a diagonal matrix.

The transpose of matrix A = A’ =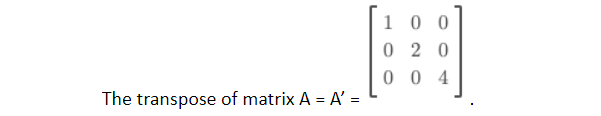

Horizontal and vertical matrix 

• A horizontal matrix is a rectangular matrix of order m × n, where m and n denote the number of rows and columns, respectively, and n > m. 

• For example,

A =

is a horizontal matrix. 

A’ =

We can observe that the transposed matrix is a vertical matrix after transposition. 

• Let m and n denote the number of rows and columns in a rectangular matrix, respectively. A vertical matrix refers to a rectangular matrix where the number of rows exceeds the number of columns.

For example, 

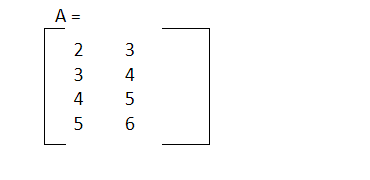
is a vertical matrix. After transposing the values of vertical matrix B, the resultant transposed matrix is horizontal. 

Conclusion 

There are several types of matrices such as row and column matrix, diagonal matrix, vertical and horizontal matrix, upper and lower triangular matrix, square matrix, zero or null matrix, and symmetric and skew-symmetric matrix, amongst many others. 

The transpose of a matrix is obtained by interchanging its rows with its columns or its columns with its rows. Therefore, the transpose of a matrix will be obtained if the elements in the first row of matrix A are written in the first column. And the elements in the second row are written in the second column, and so on.