Profile
Settings
Refer your friends
Sign out
The fundamental theorem of calculus connects the concepts of differentiation (calculating the gradient) and integration (calculating the slope or estimating the area under the curve). The two processes are inverses. They involve a constant that depends on the point where one starts computing the area.
The first portion of the theorem, commonly referred to as the first fundamental theorem of calculus, states that we can produce an antiderivative (F, also known as an indefinite integral) of a function f by integrating f with a variable bound of integration. For continuous functions, this theorem refers to the presence of antiderivatives.
The second portion of the theorem, sometimes known as the second fundamental theorem of calculus, states that we can calculate the integral of a function f over some interval using any one of its infinitely numerous antiderivatives, such as F. This aspect of the theorem is useful in practice since it avoids using numerical integration to compute integrals by explicitly calculating the antiderivative of a function via symbolic integration.
Fundamental Theorem of Calculus Part 1: Integrals and Antiderivatives
As previously stated, the first part of the fundamental theorem of calculus explains the link between differentiation and integration. It provides a method for evaluating definite integrals without using Riemann sums or computing areas. Part 1 established the connection between differentiation and integration.
If f(x) is a continuous function across the interval [a,b], and F(x) is defined by
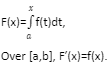
Before we go into the proof, there are a few things to consider.
First, a couple of words or two about the notation: it is worth noting that we have defined F(x) as the definite integral of another function, f(t), from point a to point x. At first appearance, this definition is perplexing because we have already said that a definite integral is a number, but it appears to be a function here.
The important thing to remember here is that a definite integral is a number for any given value of x. For any value of x, the function F(x) produces a number (the value of the definite integral).
Second, some important ramifications of this theorem are worth discussing. It is named the fundamental theorem of calculus for a reason.
It links integration and differentiation and ensures the existence of an antiderivative for any integrable function. It ensures that any continuous function has an antiderivative in particular.
Fundamental Theorem of Calculus, Part 2: The Evaluation Theorem
The second fundamental theorem of calculus is possibly the most important in calculus. After 500 years of hard work by mathematicians, new techniques arose that gave scientists the tools they needed to explain a wide range of occurrences.
Astronomers could now measure distances in space and map planetary orbits using calculus. Simple and accurate solutions to everyday financial challenges such as estimating marginal costs and predicting total profit are now possible.
Engineers could determine a material’s bending strength or three-dimensional motion. Calculus forever altered our perspective of the world.
Using this theorem is simple after calculating approximate areas by adding the areas of n rectangles. We can compute the area of an entire curved region by evaluating an antiderivative at the first and last endpoints of an interval, which appears almost too simple.
F(x) is any antiderivative of f(x) if f is continuous throughout the interval [a,b] and F(x) is any antiderivative of f(x).
The notation F(x)|ba is frequently used to represent F(b)F. (a). This vertical bar, along with the related limits a and b, indicates that we should evaluate the function F(x) at the upper limit (in this example, b) and deduct the value of the function F(x) evaluated at the lower limit (in this case, a) (in this case, a).
The second part of the fundamental theorem of calculus is also known as the evaluation theorem. It asserts that we can evaluate the definite integral if we can find an antiderivative for it. We can do this calculation by using the antiderivative at the interval’s ends and subtracting it from the definite integral.
Conclusion
Here we learned about the fundamental theorem of calculus in detail. The article provides a comprehensive introduction to the calculus theorem.
Further, we explored part 1 of the theorem that includes antiderivatives and integrals. Part 2 contains information about the evaluation of the theorem.
These notes are important. Hence, learn the points and definitions carefully.
