Operations on Matrices

A matrix is a set of numbers arranged in rows and columns to form a rectangular array. Rows are the horizontal lines, and columns are the vertical lines. The size of a matrix is defined by the number of rows and columns it contains. A matrix with m rows and n columns is called an m × n matrix. Each number in a matrix can be expressed in the form of [a]ij – where i represents the row number and j represents the column number.

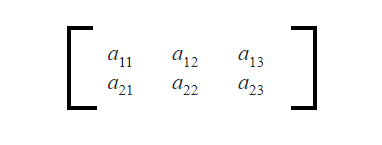
Equal Matrix

Matrices are said to be equal if the order of the matrices is equal, and each element of one matrix is equal to the corresponding element of the other matrix. In other words, the number of rows and the number of columns of matrices are equal in addition to their corresponding elements.

Matrix Operations

A matrix operation includes arithmetic operations like addition, subtraction and multiplication. These operations help us to combine two or more matrices. Also, some operations like transpose and inverse of the matrix change the matrix itself.

Matrix Addition

The matrix addition can be performed on the matrices having the same order. The addition can be performed simply by adding the corresponding elements of the matrices. If A = [aij] and B = [bij] are both m x n matrices, then their sum, A + B = [aij] + [bij]. The order of the resulting matrix is the same as the order of the matrices being added.

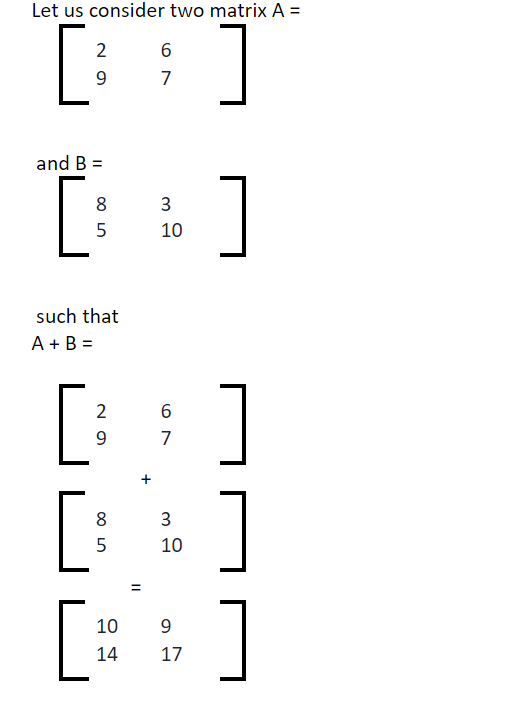
Matrix Subtraction

The matrix subtraction can also be performed on the matrices having the same order. The subtraction is performed by subtracting the corresponding elements of the matrices. If A = [aij] and B = [bij] are both m x n matrices, then their sum, A – B = [aij] – [bij].

Matrix Multiplication

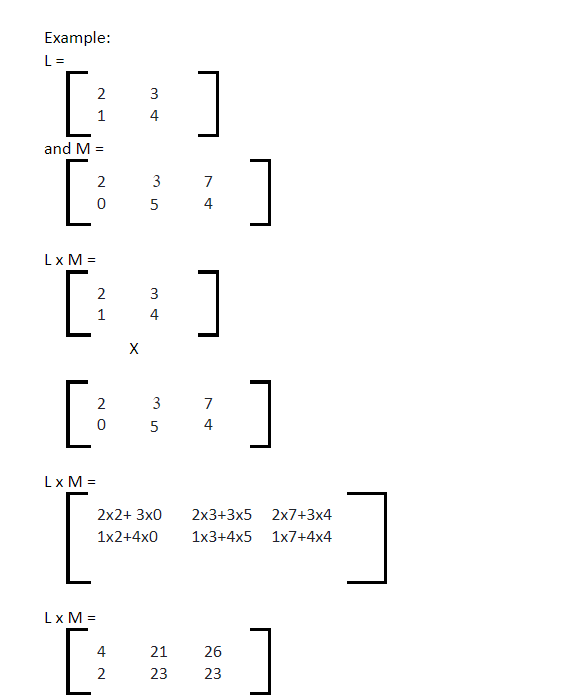
Matrix multiplication is different from subtraction and addition; corresponding elements of the same row and column are not multiplied. In order to perform matrix multiplication, the primary condition is that the number of columns in the first matrix should be equal to the number of rows in the second matrix. Let us understand the matrix multiplication by taking two matrices, A and B, which are multiplied to produce a new matrix, C.

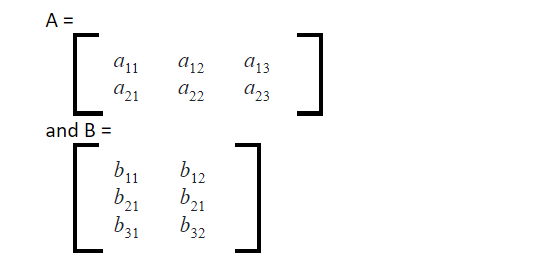
Here the number of columns of matrix A is equal to the number of rows of matrix B, so it satisfies the condition of multiplication. Now, for finding the elements of matrix C –

1. Matrix A element in row 1, column 1 will be multiplied with matrix B element in row 1, column 1 = a11 × b11.
2. Matrix A element in row 1, column 2 will be multiplied with matrix B element in row 2, column 1 = a12 × b21.
3. Matrix A element in row 1, column 3 will be multiplied with matrix B element in row 3, column 1 = a13 × b31.
4. Adding both products calculated above will give the matrix C element at row 1, column 1 = c11 = a11 × b11 + a12 × b21 + a13 x b31.

Applying similar operations on row 1 of matrix A and column 2 of matrix B will give the element in the first row and second column of matrix C (c12).

Order of the Obtained Matrix

The order of the matrix obtained by multiplying the two compatible matrices will be equal to the order of the obtained matrix.The number of the rows of matrix 1 and the number of columns of matrix 2 is the order of the matrix.

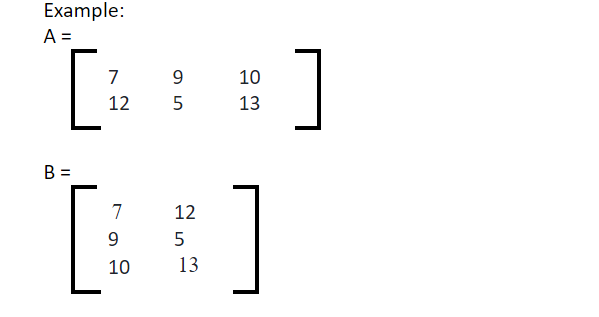
Transpose of Matrix

The transpose of a matrix is a matrix obtained by interchanging the rows with columns and columns with rows. It is denoted by ‘AT‘. In transpose of the matrix, the order of the matrix is reversed. If the order of the matrix is m x n, then after its transpose, its order becomes n x m.

Conclusion

Matrices are rectangular arrays formed by arranging the sets of numbers in rows and columns. Different operations like addition, subtraction, multiplication can be performed on a matrix. We have also learned about the transpose of the matrix, which changes the matrix itself.